题目内容
边长为2的正六边形的面积是
- A.
- B.
- C.
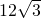
- D.
A
分析：根据题意画出图形，由正六边形的特点求出∠AOB的度数及OG的长，再由△OAB的面积即可求解．
解答：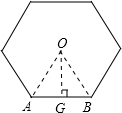
解：∵此多边形为正六边形，
∴∠AOB=
=60°；
∵OA=OB，
∴△OAB是等边三角形，
∴OA=AB=2，
∴OG=OA•cos30°=2×=
，
∴S△OAB=
×AB×OG=×2×=，
∴S六边形=6S△OAB=6×=6．
故选：A．
点评：此题考查了学生对正多边形的概念掌握和计算的能力，不仅要熟悉正六边形的性质，还要熟悉正三角形的面积公式．
分析：根据题意画出图形，由正六边形的特点求出∠AOB的度数及OG的长，再由△OAB的面积即可求解．
解答：
解：∵此多边形为正六边形，∴∠AOB=
=60°；∵OA=OB，
∴△OAB是等边三角形，
∴OA=AB=2，
∴OG=OA•cos30°=2×
=，∴S△OAB=
×AB×OG=×2×=，∴S六边形=6S△OAB=6×
=6．故选：A．
点评：此题考查了学生对正多边形的概念掌握和计算的能力，不仅要熟悉正六边形的性质，还要熟悉正三角形的面积公式．
练习册系列答案
相关题目
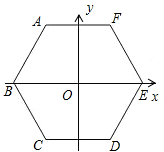如图，边长为2cm的正六边形ABCDEF的中心在坐标原点上，点B在x轴的负半轴上．
宏达广告公司设计员刘斌在设计一个广告图案，他先在纸上画了一个边长为1分米的正六边形，然后连接相隔一点的两顶点得到如图所示的对称图案．他发现中间也出现了一个正六边形，则中间的正六边形的面积是
分米2
分米2
分米2