Question

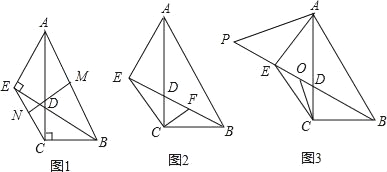
【题目】如图所示，四边形ABCD中，，对角线AC、BD交于点E，且，，若，，则CE的长为_____．

Answer 1

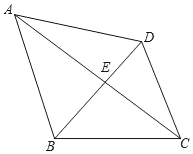
【答案】

【解析】

此题有等腰三角形，所以可作BH⊥CD，交EC于点G，利用三线合一性质及邻补角互补可得∠BGD=120°，根据四边形内角和360°，得到∠ABG+∠ADG=180°．此时再延长GB至K，使AK=AG，构造出等边△AGK．易证△ABK≌△ADG，从而说明△ABD是等边三角形，BD=AB=，根据DG、CG、GH线段之间的关系求出CG长度，在Rt△DBH中利用勾股定理及三角函数知识得到∠EBG的正切值，然后作EF⊥BG，求出EF，在Rt△EFG中解出EG长度，最后CE=CG+GE求解．

如图，作于H，交AC于点G，连接DG．

∵，

∴BH垂直平分CD，

∴，

∴，

∴，

∴，

延长GB至K，连接AK使，则是等边三角形，

∴，

又，

∴≌（），

∴，

∴是等边三角形，

∴，

设，则，，

∴，

∴，

在中，，解得，，

当时，，所以，

∴，，，

作，设，，，，，

∴，，

∴，则，

故答案为：