ЬтФПФкШн
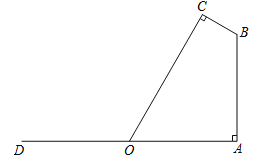
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ЃЈaЁй0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвOA=2ЃЌOB=8ЃЌOC=6ЃЎ
ЃЈaЁй0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвOA=2ЃЌOB=8ЃЌOC=6ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуMДгAЕуГіЗЂЃЌдкЯпЖЮABЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђBЕудЫЖЏЃЌЭЌЪБЃЌЕуNДгBГіЗЂЃЌдкЯпЖЮBCЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђCЕудЫЖЏЃЌЕБЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЭЃжЙдЫЖЏЃЌЕБЁїMBNДцдкЪБЃЌЧѓдЫЖЏЖрЩйУыЪЙЁїMBNЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧЖрЩйЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЁїMBNУцЛ§зюДѓЪБЃЌдкBCЩЯЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїBPCЕФУцЛ§ЪЧЁїMBNУцЛ§ЕФ9БЖЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉдЫЖЏ
ЃЛЃЈ2ЃЉдЫЖЏ![]() УыЪЙЁїMBNЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ
УыЪЙЁїMBNЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ![]() ЃЛЃЈ3ЃЉPЃЈ3ЃЌ
ЃЛЃЈ3ЃЉPЃЈ3ЃЌ ![]() ЃЉЛђЃЈ5ЃЌ
ЃЉЛђЃЈ5ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЯпЖЮЕФГЄЖШЕУГіЕуAЁЂBЁЂCЕФзјБъЃЌШЛКѓАбAЁЂBЁЂCШ§ЕуЕФзјБъЗжБ№ДњШы![]() ЃЌНтЗНГЬзщЃЌМДПЩЕУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЌНтЗНГЬзщЃЌМДПЩЕУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшдЫЖЏЪБМфЮЊtУыЃЌдђMB=6Љ3tЃЌШЛКѓИљОнЁїBHNЁзЁїBOCЃЌЧѓЕУNH=![]() tЃЌдйРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНСаГіSЁїMBNгыtЕФКЏЪ§ЙиЯЕЪНSЁїMBN=Љ
tЃЌдйРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНСаГіSЁїMBNгыtЕФКЏЪ§ЙиЯЕЪНSЁїMBN=Љ![]() ЃЈtЉ
ЃЈtЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌРћгУЖўДЮКЏЪ§ЕФЭМЯѓаджЪНјааНтД№ЃЛ
ЃЌРћгУЖўДЮКЏЪ§ЕФЭМЯѓаджЪНјааНтД№ЃЛ
ЃЈ3ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓЕУжБЯпBCЕФНтЮіЪНЮЊ![]() ЃЎгЩЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЩшЕуPЕФзјБъЮЊЃЈmЃЌ
ЃЎгЩЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЩшЕуPЕФзјБъЮЊЃЈmЃЌ ![]() ЃЉЃЎЙ§ЕуPзїPEЁЮyжсЃЌНЛBCгкЕуEЃЎНсКЯвбжЊЬѕМўКЭЃЈ2ЃЉжаЕФНсЙћЧѓЕУSЁїPBC=
ЃЉЃЎЙ§ЕуPзїPEЁЮyжсЃЌНЛBCгкЕуEЃЎНсКЯвбжЊЬѕМўКЭЃЈ2ЃЉжаЕФНсЙћЧѓЕУSЁїPBC=![]() ЃЎдђИљОнЭМаЮЕУЕНSЁїPBC=SЁїCEP+SЁїBEP=
ЃЎдђИљОнЭМаЮЕУЕНSЁїPBC=SЁїCEP+SЁїBEP=![]() EPm+
EPm+![]() EPЃЈ8ЉmЃЉЃЌАбЯрЙиЯпЖЮЕФГЄЖШДњШыЭЦжЊЃК
EPЃЈ8ЉmЃЉЃЌАбЯрЙиЯпЖЮЕФГЄЖШДњШыЭЦжЊЃК ![]() =
=![]() ЃЎ
ЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЁпOA=2ЃЌOB=8ЃЌOC=6ЃЌЁрИљОнКЏЪ§ЭМЯѓЕУAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ8ЃЌ0ЃЉЃЌCЃЈ0ЃЌ6ЃЉЃЌИљОнЬтвтЕУЃК 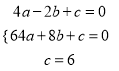 ЃЌНтЕУЃК
ЃЌНтЕУЃК 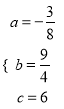 ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊ
ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊ
ЃЈ2ЃЉЩшдЫЖЏЪБМфЮЊtУыЃЌдђAM=3tЃЌBN=tЃЌЁрMB=10Љ3tЃЎгЩЬтвтЕУЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЎдкRtЁїBOCжаЃЌBC=![]() =10ЃЎШчЭМЃЌЙ§ЕуNзїNHЁЭABгкЕуHЃЌЁрNHЁЮCOЃЌЁрЁїBHNЁзЁїBOCЃЌЁр
=10ЃЎШчЭМЃЌЙ§ЕуNзїNHЁЭABгкЕуHЃЌЁрNHЁЮCOЃЌЁрЁїBHNЁзЁїBOCЃЌЁр![]() ЃЌМД
ЃЌМД![]() ЃЌЁрHN=
ЃЌЁрHN=![]() tЃЌЁрSЁїMBN=
tЃЌЁрSЁїMBN=![]() MBHN=
MBHN=![]() ЃЈ10Љ3tЃЉ
ЃЈ10Љ3tЃЉ![]() t=
t=![]() =Љ
=Љ![]() ЃЈtЉ
ЃЈtЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌЕБЁїMBNДцдкЪБЃЌ0ЃМtЃМ2ЃЌЁрЕБt=
ЃЌЕБЁїMBNДцдкЪБЃЌ0ЃМtЃМ2ЃЌЁрЕБt=![]() ЪБЃЌSЁїMBNзюДѓ=
ЪБЃЌSЁїMBNзюДѓ=![]() ЃЎ
ЃЎ
Д№ЃКдЫЖЏ![]() УыЪЙЁїMBNЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ
УыЪЙЁїMBNЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ![]() ЃЛ
ЃЛ
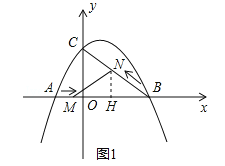
ЃЈ3ЃЉЩшжБЯпBCЕФНтЮіЪНЮЊy=kx+cЃЈkЁй0ЃЉЃЎ
АбBЃЈ8ЃЌ0ЃЉЃЌCЃЈ0ЃЌ6ЃЉДњШыЃЌЕУЃК ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК 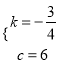 ЃЌЁржБЯпBCЕФНтЮіЪНЮЊ
ЃЌЁржБЯпBCЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЁпЕуPдкХзЮяЯпЩЯЃЌЁрЩшЕуPЕФзјБъЮЊЃЈmЃЌ ![]() ЃЉЃЌШчЭМЃЌЙ§ЕуPзїPEЁЮyжсЃЌНЛBCгкЕуEЃЌдђEЕуЕФзјБъЮЊЃЈmЃЌ
ЃЉЃЌШчЭМЃЌЙ§ЕуPзїPEЁЮyжсЃЌНЛBCгкЕуEЃЌдђEЕуЕФзјБъЮЊЃЈmЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
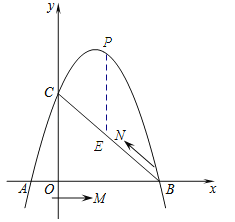
ЁрEP=![]() ЉЃЈ
ЉЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌЕБЁїMBNЕФУцЛ§зюДѓЪБЃЌSЁїPBC=9 SЁїMBN=
ЃЌЕБЁїMBNЕФУцЛ§зюДѓЪБЃЌSЁїPBC=9 SЁїMBN=![]() ЃЌЁрSЁїPBC=SЁїCEP+SЁїBEP=
ЃЌЁрSЁїPBC=SЁїCEP+SЁїBEP=![]() EPm+
EPm+![]() EPЃЈ8ЉmЃЉ=
EPЃЈ8ЉmЃЉ=![]() ЁС8EP=4ЁСЃЈ
ЁС8EP=4ЁСЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЎНтЕУm1=3ЃЌm2=5ЃЌЁрPЃЈ3ЃЌ
ЃЎНтЕУm1=3ЃЌm2=5ЃЌЁрPЃЈ3ЃЌ ![]() ЃЉЛђЃЈ5ЃЌ
ЃЉЛђЃЈ5ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ