题目内容
已知直角三角形两边x、y的长满足|x2-9|+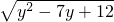 =0,则第三边的长为________.
=0,则第三边的长为________.
3 ,5或
,5或
分析:此题考查了非负数的性质,即若几个非负数的和为零,则每个非负数都为零,即可得到方程组,解方程组即可求得直角三角形的两边长,此时还要注意此两边可能都是直角边,也可能一个是直角边一个是斜边,注意别漏解.
解答:∵|x2-9|+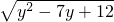 =0,
=0,
∴x2-9=0且y2-7y+12=0,
∴x=±3,y1=3,y2=4,
∵x,y是三角形的边长,
∴x=3,y1=3,y2=4,
(1)当x=3,y=3是两直角边时,斜边长=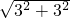 =3
=3 ,
,
(2)当x=3,y=4是两直角边时,斜边长= =5,
=5,
(3)当x=3是直角边,y=4是斜边时,另一直角边长为 =
= ,
,
所以第三边的长为3 ,5或
,5或 ,
,
故答案为:3 ,5或
,5或 .
.
点评:本题考查了勾股定理在直角三角形中的运用,考查了绝对值、算术平方根的非负数的性质,考查了分类讨论思想,本题中讨论边长为4的边是直角边还是斜边是解题的关键.
 ,5或
,5或
分析:此题考查了非负数的性质,即若几个非负数的和为零,则每个非负数都为零,即可得到方程组,解方程组即可求得直角三角形的两边长,此时还要注意此两边可能都是直角边,也可能一个是直角边一个是斜边,注意别漏解.
解答:∵|x2-9|+
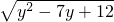 =0,
=0,∴x2-9=0且y2-7y+12=0,
∴x=±3,y1=3,y2=4,
∵x,y是三角形的边长,
∴x=3,y1=3,y2=4,
(1)当x=3,y=3是两直角边时,斜边长=
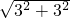 =3
=3 ,
,(2)当x=3,y=4是两直角边时,斜边长=
 =5,
=5,(3)当x=3是直角边,y=4是斜边时,另一直角边长为
 =
= ,
,所以第三边的长为3
 ,5或
,5或 ,
,故答案为:3
 ,5或
,5或 .
.点评:本题考查了勾股定理在直角三角形中的运用,考查了绝对值、算术平方根的非负数的性质,考查了分类讨论思想,本题中讨论边长为4的边是直角边还是斜边是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
已知直角三角形两边长分别为6和8,则另一条边长为( )
| A、10 | ||
| B、28 | ||
C、2
| ||
D、10或2
|