题目内容
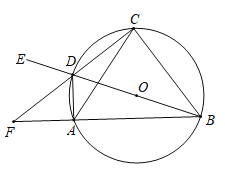
【题目】如图,⊙![]() 是四边形
是四边形![]() 的外接圆,
的外接圆,![]() 是四边形
是四边形![]() 的对角线, BD经过圆心O,点
的对角线, BD经过圆心O,点![]() 在BD的延长线上,BA与CD的延长线交于点F,DF平分
在BD的延长线上,BA与CD的延长线交于点F,DF平分![]()
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,⊙
,⊙![]() 半径为5,求
半径为5,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)30°;(3)6![]()
【解析】
(1)根据角平分线的定义得到∠EDF=∠ADF,根据圆内接四边形的性质和圆周角定理结论得到结论;
(2)根据圆周角定理得到AD⊥BF,推出△ACB是等边三角形,得到∠ADB=∠ACB=60°,根据等腰三角形的性质得到结论;
(3)设CD=k,BC=2k,根据勾股定理得到BD= ![]() ,求得=2
,求得=2![]() ,BC=AC=4
,BC=AC=4![]() ,根据相似三角形的性质即可得到结论
,根据相似三角形的性质即可得到结论
(1)证明:∵DF平分∠ADE,
∴∠EDF=∠ADF,
∵∠EDF=∠ABC,∠BAC∠BDC,∠EDF=∠BDC,
∴∠BAC=∠ABC,
∴AC=BC;
(2)解:∵BD是⊙O的直径,
∴AD⊥BF,
∵AF=AB,
∴DF=DB,
∴∠FDA=∠BDA,
∴∠ADB=∠CAB=∠ACB,
∴△ACB是等边三角形,
∴∠ADB=∠ACB=60°,
∴∠ABD=90°-60°=30°,
∴∠F=∠ABD=30°;
(3)解:∵![]() ,
,
∴![]() ,
,
设CD=k,BC=2k,
∴BD= ![]() ,
,
∴k=2![]() ,
,
∴CD=2![]() ,BC=AC=4
,BC=AC=4![]() ,
,
∵∠ADF=∠BAC,
∴∠FAC=∠ADC,
∵∠ACF=∠DCA,
∴△ACF∽△DCA,
∴![]() ,
,
∴CF=8![]() ,
,
∴DF=CF-CD=6![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目