题目内容
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,P为弧BC上一点,则cos∠APD为________.
如图,已知点A、B、C、D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,P为弧BC上一点,则cos∠APD为________.

分析:由AD∥BC,AC平分∠BCD,∠ADC=120°,得到∠1=∠2=30°;然后由圆周角定理求得∠1=∠APD,从而求得cos∠APD=cos∠1=cos30°=
 .
.解答:
 解:如图,
解:如图,∵AC平分∠BCD(已知),
∴∠1=∠2;
又∵AD∥BC(已知),∠ADC=120°,
∴∠BCD=60°(两直线平行,同旁内角互补),
∴∠1=∠2=30°,
∴∠1=∠APD(同弧所对的圆周角相等),
∴cos∠APD=cos∠1=cos30°=
 .
.故答案是:

点评:本题考查了圆周角定理,特殊角的三角函数值.根据平行线的性质和角平分线的性质求得∠1=30°是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )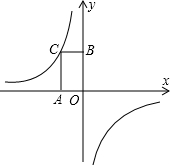 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=