��Ŀ����
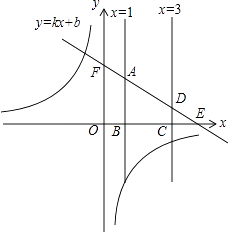
����Ŀ����֪����������y= ![]() ��ͼ���ڵڶ��������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D����A��D���ڵ�һ���ޣ�ֱ��y=kx+b��x�ύ�ڵ�E����y�ύ�ڵ�F
��ͼ���ڵڶ��������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D����A��D���ڵ�һ���ޣ�ֱ��y=kx+b��x�ύ�ڵ�E����y�ύ�ڵ�F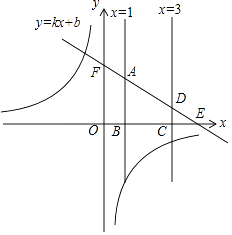
��1���� ![]() =
= ![]() �ҡ�OFE���������
�ҡ�OFE��������� ![]() ʱ�������һ�κ����Ľ���ʽ��
ʱ�������һ�κ����Ľ���ʽ��
��2���ڣ�1���������£����ݺ���ͼ������ʽ ![]() ��kx+b�Ľ⼯��
��kx+b�Ľ⼯��
���𰸡�
��1���⣺������ã� ![]() ��
��
��BC=2��BE=EC+BC��
�� ![]() ��
��
��BE=8��
��OE=9����E��9��0����
�ߵ�F������Ϊ��0��b����
��S��OFE= ![]() ��9��b=
��9��b= ![]() ��
��
���b=3��
��һ�κ���y=kx+3������E��9��0�����ɵ�
k=�� ![]() ��
��
��һ�κ����Ľ���ʽΪy=�� ![]() x+3��
x+3��
��2���⣺� ![]() =��
=�� ![]() x+3��
x+3��
���x1= ![]() ��x2=
��x2= ![]() ��
��
��ֱ��y=kx+b�뷴��������y= ![]() �Ľ�������ĺ�������
�Ľ�������ĺ������� ![]() ��
�� ![]() ��
��
���ʽ ![]() ��kx+b�Ľ⼯Ϊ
��kx+b�Ľ⼯Ϊ ![]() ��x��0��x��
��x��0��x�� ![]() ��
��
����������1����������ó�E������꣬�ٸ���S��OFE= ![]() �����ɵõ�b��ֵ���ٸ���һ�κ���y=kx+b��b��0��������E���ɵ�K��ֵ����2����������������Ľ������꣬�ٸ��ݲ���ʽ
�����ɵõ�b��ֵ���ٸ���һ�κ���y=kx+b��b��0��������E���ɵ�K��ֵ����2����������������Ľ������꣬�ٸ��ݲ���ʽ ![]() ��kx+b�ļ������壬���ɵó����ۡ�
��kx+b�ļ������壬���ɵó����ۡ�

 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�




