题目内容
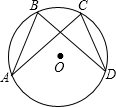如图，点A、B、C、D在⊙O上，AB=DC，AC与BD相等吗？为什么？
解：AC与BD相等．
理由如下：∵AB=DC，
∴弧AB=弧CD，
∴弧AB+弧BC=弧BC+弧CD，
即弧AC=弧BD，
∴AC=BD．
分析：由AB=DC，根据在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等得到弧AB=弧CD，即有弧AB+弧BC=弧BC+弧CD，即弧AC=弧BD，因此AC与BD相等．
点评：本题考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等．在圆中经常利用此结论把圆心角、弧、弦之间进行转化．
理由如下：∵AB=DC，
∴弧AB=弧CD，
∴弧AB+弧BC=弧BC+弧CD，
即弧AC=弧BD，
∴AC=BD．
分析：由AB=DC，根据在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等得到弧AB=弧CD，即有弧AB+弧BC=弧BC+弧CD，即弧AC=弧BD，因此AC与BD相等．
点评：本题考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等．在圆中经常利用此结论把圆心角、弧、弦之间进行转化．
练习册系列答案
阅读快车系列答案
相关题目
BE、CD、CE，已知∠BED=30°．
如图，点A的坐标为（2| 2 |
| A、（0，0） | ||||||||
B、(
| ||||||||
| C、（1，1） | ||||||||
D、(
|
12、如图，点O到直线l的距离为3，如果以点O为圆心的圆上只有两点到直线l的距离为1，则该圆的半径r的取值范围是