题目内容
花园小区有一朝向为正南方向的居民楼（如图），该居民楼的一楼是高4米的小区商场，商场以上是居民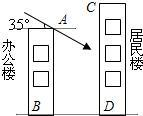
住房．在该楼的前面16米处要盖一栋高18米的办公楼．当冬季正午的阳光与水平线的夹角为35°时，问：（1）商场以上的居民住房采光是否有影响，为什么？
（2）若要使商场采光不受影响，两楼应相距多少米？（结果保留一位小数）
（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
分析：（1）求是否影响采光，就是求办公楼的影子部分是否高过商场的高度，如果设光线交居民楼于E，那么就是求DE的长度，通过做EF∥BD即EF⊥AB，来构建直角三角形，那么AF的长度就可以在直角三角形AFE中求出，DE=AB-AF，这样就能判断出是否影响采光了．
（2）要想商场采光不受影响，那么办公楼的高度就要与其影子的高度相等，即AB=BD，在直角三角形ABD中，有AB的长，∠BAD也容易求得，那么BD的值也就不难求得了．
（2）要想商场采光不受影响，那么办公楼的高度就要与其影子的高度相等，即AB=BD，在直角三角形ABD中，有AB的长，∠BAD也容易求得，那么BD的值也就不难求得了．
解答：
解：（1）如图，光线交CD于点E，过点E作EF∥BD交AB于点F．
设DE=x米，则AF=（18-x）米
在Rt△AFE中，∵∠AEF=35°．
∴tan35°=
．
即：0.70=
．
∴x=6.8
∵6.8＞4．
答：居民住房的采光有影响．
（2）如图，在Rt△ABD中，tan∠ADB=
．
∴tan35°=
．
∴BD=
≈25.8米．
答：两楼相距25.8米．
解：（1）如图，光线交CD于点E，过点E作EF∥BD交AB于点F．设DE=x米，则AF=（18-x）米
在Rt△AFE中，∵∠AEF=35°．
∴tan35°=
| AF |
| EF |
即：0.70=
| 18-x |
| 16 |
∴x=6.8
∵6.8＞4．
答：居民住房的采光有影响．
（2）如图，在Rt△ABD中，tan∠ADB=
| AB |
| BD |
∴tan35°=
| 18 |
| BD |
∴BD=
| 18 |
| 0.70 |
答：两楼相距25.8米．
点评：本题是将实际问题转化为直角三角形中的数学问题，可通过作辅助线构造直角三角形，再把条件和问题转化到这个直角三角形中，使问题解决．
练习册系列答案
相关题目
