题目内容
(1)观察发现
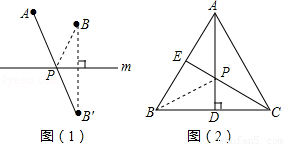
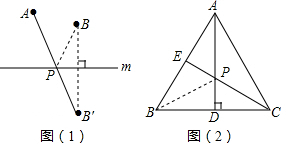
如图1,⊙O的半径为1,点P为⊙O外一点,PO=2,在⊙O上找一点M,使得PM最长.
作法如下:作射线PO交⊙O于点M,则点M就是所求的点,此时PM=______.
请说明PM最长的理由.
(2)实践运用
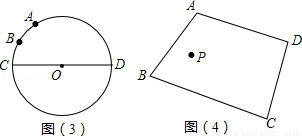
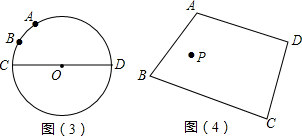
如图2,在等边三角形 ABC中,AB=2,以AB为斜边作直角三角形AMB,使CM最长.
作法如下:以AB为直径画⊙O,作射线CO交⊙O右侧于点M,则△AMB即为所求.请按上述方法用三角板和圆规画出图形,并求出CM的长度.
(3)拓展延伸
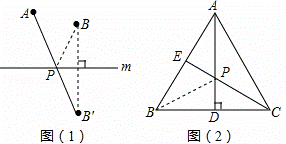
如图3,在周长为m的任意形状的△ABC中,分别以AB、AC为斜边作直角三角形AMB,直角三角形ANC,使得线段MN最长,用尺规画出图形,此时MN=______.(保留作图痕迹)
【答案】分析:(1)根据PM=PO+OM即可求出PM的长;在⊙O上任取一异于点M的点M′,连接OM′,根据三角形三边关系定理得出PM=PO+OM′>PM′;
(2)先根据作法作出△AMB,然后在直角△ACO中利用锐角三角函数求出CO= ,则CM=CO+OM=
,则CM=CO+OM= +1;
+1;
(3)先分别以AB、AC为直径画⊙O、⊙P,作射线PO交⊙O左侧于点M,延长OP交⊙P右侧于点N,此时线段MN最长;由于O、P分别为AB、AC的中点,根据三角形中位线定理即可求出MN=0.5m.
解答: 解:(1)如图1,PM=PO+OM=2+1=3.
解:(1)如图1,PM=PO+OM=2+1=3.
在⊙O上任取一异于点M的点M′,连接OM′.
在△POM′中,∵PO+OM′>PM′,
又∵PM=PO+OM=PO+OM′,
∴PM>PM′;
 (2)如图2,
(2)如图2,
在直角△ACO中,∵∠AOC=90°,∠OAC=60°,OA= AB=1,
AB=1,
∴CO= OA=
OA= ,
,
∴CM=CO+OM= +1;
+1;
(3)如图3,
∵O、P分别为AB、AC的中点,
∴OA= AB,AP=
AB,AP= AC,OP=
AC,OP= BC,
BC,
∴OA+AP+OP= (AB+AC+BC)=
(AB+AC+BC)= m,
m,
∴MN=MO+OP+PN=OA+OP+AP=0.5m.
故答案为3,0.5m.
点评:本题考查了圆的综合题,其中涉及到三角形三边关系定理,直角三角形的性质,三角形中位线的性质,圆的性质等知识,难度中等,正确作出图形是解题的关键.
(2)先根据作法作出△AMB,然后在直角△ACO中利用锐角三角函数求出CO=
 ,则CM=CO+OM=
,则CM=CO+OM= +1;
+1;(3)先分别以AB、AC为直径画⊙O、⊙P,作射线PO交⊙O左侧于点M,延长OP交⊙P右侧于点N,此时线段MN最长;由于O、P分别为AB、AC的中点,根据三角形中位线定理即可求出MN=0.5m.
解答:
 解:(1)如图1,PM=PO+OM=2+1=3.
解:(1)如图1,PM=PO+OM=2+1=3.在⊙O上任取一异于点M的点M′,连接OM′.
在△POM′中,∵PO+OM′>PM′,
又∵PM=PO+OM=PO+OM′,
∴PM>PM′;
 (2)如图2,
(2)如图2,在直角△ACO中,∵∠AOC=90°,∠OAC=60°,OA=
 AB=1,
AB=1,∴CO=
 OA=
OA= ,
,∴CM=CO+OM=
 +1;
+1;(3)如图3,

∵O、P分别为AB、AC的中点,
∴OA=
 AB,AP=
AB,AP= AC,OP=
AC,OP= BC,
BC,∴OA+AP+OP=
 (AB+AC+BC)=
(AB+AC+BC)= m,
m,∴MN=MO+OP+PN=OA+OP+AP=0.5m.
故答案为3,0.5m.
点评:本题考查了圆的综合题,其中涉及到三角形三边关系定理,直角三角形的性质,三角形中位线的性质,圆的性质等知识,难度中等,正确作出图形是解题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目


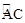 的度数为60°,点B是
的度数为60°,点B是
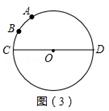

 的度数为60°,点B是
的度数为60°,点B是