题目内容
(1)树的高度与树生长的年数有关,测得某棵树的有关数据如下表(树苗原高100厘米):
| 年数a | 高度h(单位:厘米) |
| 1 | 115 |
| 2 | 130 |
| 3 | 145 |
| 4 | |
| … | … |
①请用含a的代数式表示:a年后树的高度h=______;
②根据这种长势,10年后这棵树可能达到的高度是______厘米.
(2)观察如图的图形

①第38个图形是什么颜色?______
②第19个图形是几边形?______.
解:(1)第4年树苗可能达到的高度是145+15=160(厘米);
②a年后树的高度h=115+15(a-1)=100+15a;
③当a=10时,则h=100+150=250(厘米);
(2)①第38个图形是黑色;
②19=2×9+1,则第19个图形的边数是9+3=12.
故答案为160;100+15a;250;黑色;12.
分析:(1)从表格中,可以发现,下一年总比上一年的高度增长15厘米;
①根据(1)中发现的规律进行推广;
②把a=10代入②中发现的规律即可;
(2)①根据黑白相间的规律,知第奇数个图形是白色,第偶数个图形是黑色;
②观察发现,第一个和第二个都是三角形,第三个和第四个都是四边形,根据图形的边数是成对出现的,即可判断.
点评:此题考查的是一道图形的基本规律,能够从特殊数值中发现规律,进而推广.
②a年后树的高度h=115+15(a-1)=100+15a;
③当a=10时,则h=100+150=250(厘米);
(2)①第38个图形是黑色;
②19=2×9+1,则第19个图形的边数是9+3=12.
故答案为160;100+15a;250;黑色;12.
分析:(1)从表格中,可以发现,下一年总比上一年的高度增长15厘米;
①根据(1)中发现的规律进行推广;
②把a=10代入②中发现的规律即可;
(2)①根据黑白相间的规律,知第奇数个图形是白色,第偶数个图形是黑色;
②观察发现,第一个和第二个都是三角形,第三个和第四个都是四边形,根据图形的边数是成对出现的,即可判断.
点评:此题考查的是一道图形的基本规律,能够从特殊数值中发现规律,进而推广.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一种树的高度h(厘米)与生长年数x(年)之间的关系如下表:(树的原高80厘米)
| 生长年数x/年 | 树的高度h/厘米 |
| 1 | 80+5 |
| 2 | 80+10 |
| 3 | 80+15 |
| 4 | 80+20 |
| … | … |
(1)写出生长年数x与树的高度h的关系式;
(2)计算当树长到150cm高度时需要几年?
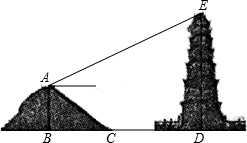 高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38,
高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38, (指坡面的铅垂高度AB与水平宽度BC的比).从山脚下的C处步行6米到达坡顶A处,测得青云塔塔顶的仰角为21度,求青云塔的
(指坡面的铅垂高度AB与水平宽度BC的比).从山脚下的C处步行6米到达坡顶A处,测得青云塔塔顶的仰角为21度,求青云塔的 高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38,
高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38, (指坡面的铅垂高度AB与水平宽度BC的比).从山脚下的C处步行6米到达坡顶A处,测得青云塔塔顶的仰角为21度,求青云塔的高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38,
(指坡面的铅垂高度AB与水平宽度BC的比).从山脚下的C处步行6米到达坡顶A处,测得青云塔塔顶的仰角为21度,求青云塔的高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38, =1.7,结果精确到1m.)
=1.7,结果精确到1m.)