题目内容
在平面直角坐标系xOy（如图）中，已知：点A（3，0）、B（-2，5）、C（0，-3）．
（1）求经过点A、B、C的抛物线的表达式；
（2）若点D是（1）中求出的抛物线的顶点，求tan∠CAD的值．
解：（1）设抛物线的解析式为y=ax2+bx+c，
把点A（3，0）、B（-2，5）、C（0，-3）代入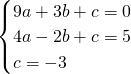得
，解得
，
所以抛物线的解析式为y=x2-2x-3；
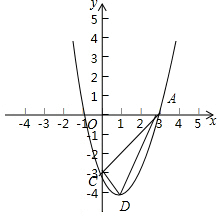（2）y=x2-2x-3=（x-1）2-4，
所以D点坐标为（1，-4），
∵AD2=（3-1）2+（0+4）2=20，
CD2=（-3+4）2+（0-1）2=2，
AC2=（3-0）2+（0+3）2=18，
∴AD2=CD2+AC2，
∴△ACD为直角三角形，
∴tan∠CAD=
=
=
．
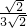分析：（1）设抛物线的解析式为y=ax2+bx+c，再把三个已知点的坐标代入得到关于a、b、c的方程组，解方程组即可得到二次函数的解析式；
（2）把（1）中的解析式配方得到顶点式y=（x-1）2-4，则D点坐标为（1，-4），再利用两点间的距离公式分别计算出AC、CD、AD，然后根据勾股定理的逆定理判断△ACD为直角三角形，再利用正切的定义求解．
点评：本题考查了用待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．也考查了勾股定理及其逆定理．
把点A（3，0）、B（-2，5）、C（0，-3）代入得
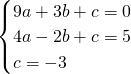，解得，所以抛物线的解析式为y=x2-2x-3；
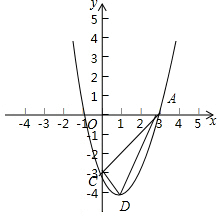（2）y=x2-2x-3=（x-1）2-4，所以D点坐标为（1，-4），
∵AD2=（3-1）2+（0+4）2=20，
CD2=（-3+4）2+（0-1）2=2，
AC2=（3-0）2+（0+3）2=18，
∴AD2=CD2+AC2，
∴△ACD为直角三角形，
∴tan∠CAD=
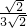==．分析：（1）设抛物线的解析式为y=ax2+bx+c，再把三个已知点的坐标代入得到关于a、b、c的方程组，解方程组即可得到二次函数的解析式；
（2）把（1）中的解析式配方得到顶点式y=（x-1）2-4，则D点坐标为（1，-4），再利用两点间的距离公式分别计算出AC、CD、AD，然后根据勾股定理的逆定理判断△ACD为直角三角形，再利用正切的定义求解．
点评：本题考查了用待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．也考查了勾股定理及其逆定理．
练习册系列答案
相关题目
如图在平面直角坐标系xoy中，正方形OABC的边长为2厘米，点A、C分别在y轴的负半轴和x轴的正半轴上．抛物线y=ax2+bx+c经过点A，B和点D（4，
x轴于点A，作BC⊥y轴于点C，点P沿OC自点O向点C运动，同时点Q沿OA向点A运动，点Q与点P的速度之比为1：n，连接PB、PQ．
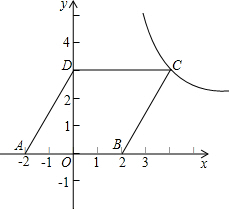（2013•甘井子区二模）如图，平行四边形ABCD放置在平面直角坐标系xOy中，已知A（-2，0），B（2，0），D（0，3），反比例函数