题目内容
若两个正数的算术平均数(即两数和的一半)为2
,几何平均数(即两数积的算术平方根)为
,则这两个数的差是( )
| 3 |
| 3 |
| A.±6 | B.6 | C.±36 | D.36 |
设这两个数分别为a和b,
则根据题意得:
=2
①,
=
②,
①②两式联立解得:a2+b2=(a+b)2-2ab=48-6=42,
∴(a-b)2=a2+b2-2ab=42-2×3=36,
∴a-b=±6.
故选A.
则根据题意得:
| a+b |
| 2 |
| 3 |
| ab |
| 3 |
①②两式联立解得:a2+b2=(a+b)2-2ab=48-6=42,
∴(a-b)2=a2+b2-2ab=42-2×3=36,
∴a-b=±6.
故选A.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 ,几何平均数(即两数积的算术平方根)为
,几何平均数(即两数积的算术平方根)为 ,则这两个数的差是
,则这两个数的差是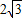 ,几何平均数(即两数积的算术平方根)为
,几何平均数(即两数积的算术平方根)为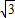 ,则这两个数的差是( )
,则这两个数的差是( )