题目内容
 某运输部门规定:办理一件物品的重量不超过akg(a<18)时,需付基础费30元和保险费3元;为限制过重物品的托运,当一件物品的重量超过akg时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某物品的重量为xkg,支付费用为y元.
某运输部门规定:办理一件物品的重量不超过akg(a<18)时,需付基础费30元和保险费3元;为限制过重物品的托运,当一件物品的重量超过akg时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某物品的重量为xkg,支付费用为y元.(1)当0≤x≤a时,y=
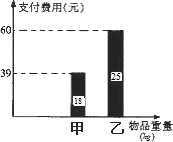
(2)甲、乙二人各托运了一件物品,物品重量与支付费用如图所示.根据以上信息确定a,b的值,并写出支付费用y(元)与每件物品重量x(kg)3的函数关系式;在物品可分拆的情况下,用不超过120元的费用能否托运50kg的物品?若能,请设计出其中二种托运方案,并求出托运费用;若不能,请说明理由.
分析:(1)不超过a千克时,只需付基础费30元和保险费3元;超过akg时,需付费:33元基础费+超过部分的费用
(2)易知这两个数据满足第二个函数解析式,把(18,39),(25,60)代入第二个函数解析式就能求得a、b的值.那么a就表示不出钱的千克数的结束,进行拆分时,应注意充分使用不出钱的千克数.
(2)易知这两个数据满足第二个函数解析式,把(18,39),(25,60)代入第二个函数解析式就能求得a、b的值.那么a就表示不出钱的千克数的结束,进行拆分时,应注意充分使用不出钱的千克数.
解答:解:(1)当0≤x≤a时,y=33,当x>a时y=33+(x-a)b(2分)
(2)①由a<18,故由图中甲、乙数据应满足y=33+(x-a)b
从而有
.解得
.(3分)
故所求函数的解析式为:
当0<x≤16时,y=33(1分)
当x>16时,y=3x-15(1分)
②能够托运,方案一:将物品拆分成两件,一件是16kg,另一件是34kg,此时费用为33+3×34-15=120元;
方案二:将物品拆分成两件,一件是25kg,另一件也是25kg,此时费用也为2×(3×25-15)=120元;
方案三:将物品拆分成三件,两件均为16kg,另一件为18kg,此时费用为2×33+(3×18-15)=105元.
(一种得1分,两种得3分)
(2)①由a<18,故由图中甲、乙数据应满足y=33+(x-a)b
从而有
|
|
故所求函数的解析式为:
当0<x≤16时,y=33(1分)
当x>16时,y=3x-15(1分)
②能够托运,方案一:将物品拆分成两件,一件是16kg,另一件是34kg,此时费用为33+3×34-15=120元;
方案二:将物品拆分成两件,一件是25kg,另一件也是25kg,此时费用也为2×(3×25-15)=120元;
方案三:将物品拆分成三件,两件均为16kg,另一件为18kg,此时费用为2×33+(3×18-15)=105元.
(一种得1分,两种得3分)
点评:解读题意,找到相应的等量关系是解决本题的关键,点在函数解析式上,就应适合这个函数解析式.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为 元(用含a的代数式表示);
当x≥16时,支付费用为 元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示:
①试根据以上提供的信息确定a,b的值;
②试问在物品可拆分的情况下,用不超过105元的费用能否托运50千克物品?若能,请设计出其中一种托运方案,并求出托运费用;若不能,请说明理由.
(1)当x≤16时,支付费用为
当x≥16时,支付费用为
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示:
| 物品重量(千克) | 支付费用(元) |
| 18 | 38 |
| 25 | 53 |
②试问在物品可拆分的情况下,用不超过105元的费用能否托运50千克物品?若能,请设计出其中一种托运方案,并求出托运费用;若不能,请说明理由.
先阅读下列一段文字,然后解答问题:
某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元;为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为 元(用含a的代数式表示);当x≥16时,支付费用为 元(用含x和a、b的代数式表示)
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
①试根据以上提供的信息确定a,b的值.
②试问在物品可拆分的情况下,用不超过120元的费用能否托运50千克物品?若能,请设计出其中一种托运方案,并求出托运费用;若不能,请说明理由.
某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元;为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
| 物品重量(千克) | 支付费用(元) |
| 18 | 39 |
| 25 | 60 |
②试问在物品可拆分的情况下,用不超过120元的费用能否托运50千克物品?若能,请设计出其中一种托运方案,并求出托运费用;若不能,请说明理由.