题目内容
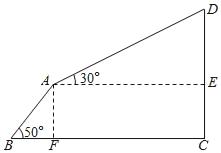
【题目】如图,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB, OA上的动点,则△CDE周长的最小值是_____________.

【答案】10
【解析】
点C关于OA的对称点C′(1,0),点C关于直线AB的对称点为C″,连接C′C″与AO交于点E,与AB交于点D,此时△CDE周长最小,这个最小值就是线段C′C″,然后求出C″的坐标即可解决问题.
解:如图,点C关于OA的对称点C′(1,0),点C关于直线AB的对称点C″,
∵直线AB的解析式为y=x+7,
∴设直线CC″的解析式为y=x+b,
代入C(1,0)得:0=1+b,
解得:b=-1,
∴直线CC″的解析式为:y=x1,
联立![]() ,解得:
,解得:![]() ,
,
∴直线AB与直线CC″的交点坐标为K(4,3),
∵K是CC″中点,
∴C″(7,6),
连接C′C″与AO交于点E,与AB交于点D,此时△CDE周长最小,
△CDE的周长=DE+EC+CD=EC′+ED+DC″=C′C″=![]() ,
,
故答案为:10.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
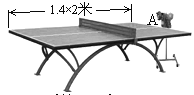
能考试全能100分系列答案【题目】(本题12分)某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为![]() (米),与桌面的高度为
(米),与桌面的高度为![]() (米),运行时间为
(米),运行时间为![]() (秒),经多次测试后,得到如下部分数据:
(秒),经多次测试后,得到如下部分数据:
| 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0. 8 | … |
| 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
(1)当![]() 为何值时,乒乓球达到最大高度?
为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,![]() 与
与![]() 满足
满足![]()
①用含![]() 的代数式表示
的代数式表示![]() ;
;
②球网高度为0.14米,球桌长(1.4×2)米,若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求![]() 的值.
的值.