题目内容

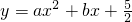如图，抛物线 $数学公式$ 与直线AB交于点A（-1，0），B（4， $数学公式$ ）．点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．
（1）求抛物线的解析式；
（2）①当D为抛物线顶点时，线段DC的长度是多少？
②设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出S的最大值．

解：（1）由题意得 $\text{[math]}$
解得： $\text{[math]}$
故抛物线解析式为：y=- $\text{[math]}$ x²+2x+ $\text{[math]}$ ；

（2）①∵y=- $\text{[math]}$ x²+2x+ $\text{[math]}$ =- $\text{[math]}$ （x-2）²+ $\text{[math]}$ ，
∴顶点 $\text{[math]}$
设直线AB为：y=kx+b，
则有 $\text{[math]}$
解得 $\text{[math]}$
∴直线解析式为： $\text{[math]}$ ，
当x=2时，y= $\text{[math]}$ ×2+ $\text{[math]}$ = $\text{[math]}$ ，
∴ $\text{[math]}$
∴ $\text{[math]}$ ，

②由题意可得：D（m， $\text{[math]}$ ），C（m， $\text{[math]}$ ），
CD=（ $\text{[math]}$ ）-（ $\text{[math]}$ ）
= $\text{[math]}$ ．
∴ $\text{[math]}$
= $\text{[math]}$ ×CD
= $\text{[math]}$ ×（ $\text{[math]}$ ）
=- $\text{[math]}$ m²+ $\text{[math]}$ m+5
=- $\text{[math]}$ （m- $\text{[math]}$ ）²+ $\text{[math]}$ ．
∵ $\text{[math]}$ ，
∴当 $\text{[math]}$ 时，S最大值为 $\text{[math]}$ ．
分析：（1）利用待定系数法求二次函数解析式即可得出答案；
（2）①利用配方法求出D点坐标，进而得出AB解析式，得出C点坐标，进而求出CD即可；
②由题意可得：D（m， $\text{[math]}$ ），C（m， $\text{[math]}$ ），进而利用△ADB的面积为△ADC的面积+△CDB的面积，求出即可．
点评：此题主要考查了二次函数的综合应用以及待定系数法求二次函数解析式和三角形面积求法等知识，利用AB解析式得出C点坐标是解题关键．

练习册系列答案

=-1，与x轴交于点C，且∠ABC=90°
求：
（1）直线AB的解析式；
（2）抛物线的解析式．

如图，抛物线与直线y=x+1交于A、C两点，与y轴交于B，AB∥x轴，且， D、E是直线y=x+1与坐标轴的交点，

（1）求抛物线的解析式；

（2）在坐标轴上找出所有的点F，使△CEF与△ABD相似，直接写出它的坐标；

（3）P为x轴上一点，Q为此抛物线上一点，是否存在P，使得以A、C、P、Q为顶点的四边形是平行四边形？若存在，请求出P点的坐标；若不存在，请说明理由．

如图，抛物线与直线AB交于x轴上的一点A，和另一点B(4，n)．点P是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线PQ与直线AB垂直，交直线AB于点Q．

(1)求抛物线的解析式和cos∠BAO的值。
(2)设点P的横坐标为用含的代数式表示线段PQ的长，并求出线段PQ长的最大值；
(3)点E是抛物线上一点，过点E作EF∥AC,交直线AB与点F,若以E、F、A、C为顶点的四边形为平行四边形，直接写出相应的点E的坐标．