Question

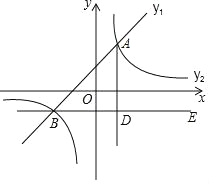
【题目】如图，在平面直角坐标系中，一次函数y1＝ax+b的图象与反比例函数y2＝的图象交于点A(1，2)和B(﹣2，m)．

(1)求一次函数和反比例函数的表达式；

(2)请直接写出y1≥y2时x的取值范围；

(3)过点B作BE∥x轴，AD⊥BE于点D，点C是直线BE上一点，若∠DAC＝30°，求点C的坐标．

Answer 1

【答案】（1）反比例函数的解析式为y2＝；一次函数解析式为y1＝x+1．（2）当﹣2≤x＜0或x≥1时，y1≥y2．（3）点C的坐标为（1﹣，﹣1）或（1+，﹣1）．

【解析】

（1）由点A的坐标，利用反比例函数图象上点的坐标特征可求出k值，由点B的横坐标利用反比例函数图象上点的坐标特征可求出m值，进而可得出点B的坐标，根据点A，B的坐标，利用待定系数法即可求出一次函数解析式；

（2）观察函数图象，由两函数图象的上下位置关系结合两交点的坐标，即可找出y1≥y2时x的取值范围；

（3）由点A，B的纵坐标可得出AD的长度及点D的坐标，在Rt△ADC中，由∠DAC＝30°可得出CD的长度，再结合点D的坐标即可求出点C的坐标．

（1）∵点A（1，2）在反比例函数y2＝的图象上，

∴2＝，

∴k＝1×2＝2，

∴反比例函数的解析式为y2＝．

∵点B（﹣2，m）在反比例函数y2＝的图象上，

∴m＝＝﹣1，

∴点B的坐标为（﹣2，﹣1）．

把A（1，2），B（﹣2，﹣1）代入y1＝ax+b得：

解得：

∴一次函数解析式为y1＝x+1．

（2）由函数图象可知：当﹣2≤x＜0或x≥1时，y1≥y2．

（3）由题意得：AD＝2﹣（﹣1）＝3，点D的坐标为（1，﹣1）．

在Rt△ADC中，tan∠DAC＝，即，

解得：CD=．

当点C在点D的左侧时，点C的坐标为（1﹣，﹣1）；

当点C在点D的右侧时，点C的坐标为（1+，﹣1）．

∴点C的坐标为（1﹣，﹣1）或（1+，﹣1）．