Question

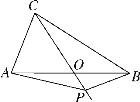
【题目】如图， 在△ABC中，AC=3、AB=4、BC=5， P为BC上一动点，PG⊥AC于点G，PH⊥AB

于点H，M是GH的中点，P在运动过程中PM的最小值为（ ）

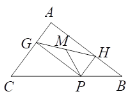
A. 2.4 B. 1.4

C. 1.3 D. 1.2

【答案】D

【解析】分析: 由AC=3、AB=4、BC=5，得AC2+AB2=BC2，则∠A=90°，再结合PG⊥AC，PH⊥AB，可证四边形AGPH是矩形；连接AP，可知当AP⊥BC时AP最短，结合矩形的两对角线相等和面积法，求出GH的值，

详解:∵AC=3、AB=4、BC=5，

∴AC2=9，AB2=16，BC2=25，

∴AC2+AB2=BC2，

∴∠A=90°.

∵PG⊥AC，PH⊥AB，

∴∠AGP=∠AHP=90° ，

∴四边形AGPH是矩形.

连接AP，

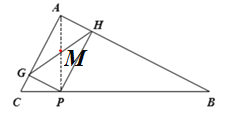
∴GH=AP.

∵当AP⊥BC时，AP最短，

∴3×4=5AP，

∴AP=，

∴PM的最小值为1.2.

故选D.

点睛: 本题考查了勾股定理的逆定理，矩形的判定与性质，垂线段最短，面积法求线段的长，需结合矩形的判定方法，矩形的性质以及三角形面积的知识求解；确定出点P的位置是解答本题的关键.

【题型】单选题
【结束】
18

【题目】计算：

（1） （2）

（3）

Answer 1

【答案】(1) ;(2) ;(3) .

【解析】（1）先化成最简二次根式，再合并同类二次根式即可；

（2）先算乘法和除法，再合并同类项或同类二次根式即可；

（3）第一项根据平方差公式计算，第二项根据完全平方公式计算，然后合并同类项或同类二次根式即可；

(1)原式==

（2）原式==

（3）原式==