题目内容

如果三角形的三边长分别为3、4和5，那么连接这个三角形三边中点，所得的三角形的周长是________．

6
分析：根据三角形的中位线定理“三角形的中位线等于第三边的一半”，易得连接这个三角形三边中点所得的三角形的三边是此三角形的三条中位线，即可得知所得的三角形的周长是原三角形周长的一半．
解答：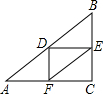

解：∵D，E，F分别是△ABC的三边的中点，
∴DE= $\text{[math]}$ AC，DF= $\text{[math]}$ BC，EF= $\text{[math]}$ AB，
∴△DEF的周长=DE+DF+EF= $\text{[math]}$ （AC+BC+AB）= $\text{[math]}$ ×（3+4+5）=6．
故答案为：6．
点评：本题考查了三角形的中位线定理：三角形的中位线等于第三边的一半．注意数形结合思想的应用．