题目内容
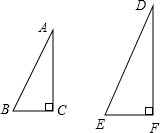如图，Rt△ABC∽Rt△DEF，∠A=35°，则∠E的度数为
- A.35°
- B.45°
- C.55°
- D.65°
C
分析：由Rt△ABC∽Rt△DEF，∠A=35°，根据相似三角形的对应角相等，即可求得∠D的度数，又由∠F=90°，即可求得∠E的度数．
解答：∵Rt△ABC∽Rt△DEF，∠A=35°，
∴∠D=∠A=35°．
∵∠F=90°，
∴∠E=55°．
故选C．
点评：此题考查了相似三角形的性质．解题的关键是掌握相似三角形的对应角相等定理的应用．
分析：由Rt△ABC∽Rt△DEF，∠A=35°，根据相似三角形的对应角相等，即可求得∠D的度数，又由∠F=90°，即可求得∠E的度数．
解答：∵Rt△ABC∽Rt△DEF，∠A=35°，
∴∠D=∠A=35°．
∵∠F=90°，
∴∠E=55°．
故选C．
点评：此题考查了相似三角形的性质．解题的关键是掌握相似三角形的对应角相等定理的应用．
练习册系列答案
相关题目
如图，Rt△ABC中，∠C=90°，BC=6cm，AC=8cm，点P从B点出发，以2cm/s的速度向点C运动，点Q从C点出发，以1cm/s的速度向点A运动．若P，Q同时出发，则经过
已知，如图，Rt△ABC中∠B=90°，Rt△DEF中∠E=90°，OF=OC，AB=6，BF=2，CE=8，CA=0，DE=15．
（2013•封开县一模）如图，Rt△ABC的直角边BC=8，AC=6