题目内容
【题目】在△ABC中，∠A＝1200，AB＝12，AC＝6，求sinB＋sinC的值.
【答案】
【解析】
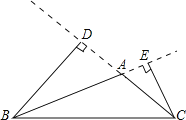
过C点作CE⊥BA交BA的延长线于E，过点B作BD⊥CA交CA的延长线于D，
过C点作CE⊥BA交BA的延长线于E，过点B作BD⊥CA交CA的延长线于D．由∠BAC=120°，求得∠EAC=60°．根据60°角的正弦求得CE=3
，AE=3，BD=6．在Rt△BCE中，根据勾股定理可得BC=6
．由此即可求得sinB＋sinC的值.
∵∠BAC=120°，
∴∠EAC=60°．
∴sin60°=
=
．
∵AC=6，AB=12，
∴CE=3，AE=3，BD=6．
在Rt△BCE中，BE=15，CE=3，
根据勾股定理可得BC=6 ．
则sinB+sinC=
=
．
练习册系列答案
相关题目
