Question

【题目】如图，射线OA的方向是北偏东15°，射线OB的方向是北偏西40°，∠AOB＝∠AOC，射线OD是OB的反向延长线．

(1)射线OC的方向是______；

(2)若射线OE平分∠COD，求∠AOE的度数；

(3)直接写出一对互余的角是______，一对互补的角是_______．

Answer 1

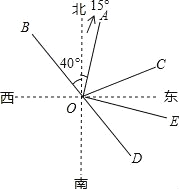
【答案】(1)北偏东70°；(2)∠AOE＝90°；(3)∠AOC与∠COE；∠AOB与∠AOD．

【解析】

（1）先求出∠AOB＝55°，再求得∠NOC的度数，即可确定OC的方向；

（2）根据射线OE平分∠COD，即可求出∠COE＝35°再利用∠AOC＝55°求出答案即可；

（3）根据余角和补角的定义即可得到结论．

解：(1)∵OB的方向是北偏西40°，OA的方向是北偏东15°，

∴∠NOB＝40°，∠NOA＝15°，

∴∠AOB＝∠NOB+∠NOA＝55°，

∵∠AOB＝∠AOC，

∴∠AOC＝55°，

∴∠NOC＝∠NOA+∠AOC＝70°，

∴OC的方向是北偏东70°；

故答案为：北偏东70°；

(2)∵∠AOB＝55°，∠AOC＝∠AOB，

∴∠BOC＝110°，

又∵射线OD是OB的反向延长线，

∴∠BOD＝180°，

∴∠COD＝180°﹣110°＝70°，

∵OE平分∠COD，

∴∠COE＝35°．

∵∠AOC＝55°，

∴∠AOE＝90°；

(3)∵∠AOE＝∠AOC+∠COE＝90°，∠AOB+∠AOD＝180°，

∴一对互余的角是∠AOC与∠COE，一对互补的角是∠AOB与∠AOD．

故答案为：∠AOC与∠COE，∠AOB与∠AOD．