题目内容
9.计算:$\frac{1}{1}$+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+3+…+100}$.分析 通过观察,分母是连续自然数的和,并逐渐增多,因此分母部分运用高斯求和公式表示出来.进一步运用拆分的方法,使计算简便.
解答 解:$\frac{1}{1}$+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+3+…+100}$
=1+$\frac{1}{\frac{(1+2)×2}{2}}$+$\frac{1}{\frac{(1+3)×3}{2}}$+…+$\frac{1}{\frac{(1+100)×100}{2}}$
=1+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{100×101}$
=1+2×($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{100}$-$\frac{1}{101}$)
=1+2×($\frac{1}{2}$-$\frac{1}{101}$)
=1+1-$\frac{2}{101}$
=1$\frac{99}{101}$
点评 此类问题,如果分母之间存在某种特殊规律时,根据规律,运用运算技巧,进行简便计算.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.把两块三角板按如图所示那样拼在一起,则∠ABC等于( )
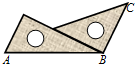

| A. | 70° | B. | 90° | C. | 105° | D. | 120° |
17.阳阳上学时先向东走,再向北走就能到学校,学校在阳阳家的( )


| A. | 东面 | B. | 背面 | C. | 东北面 | D. | 西南面 |
18.第一根绳子长M米,比第二根绳子的4倍少N米,第二根绳子的长度可以表示为( )
| A. | 4M-N | B. | M÷4-N | C. | (M+N)÷4 | D. | (M-N)÷4 |