题目内容
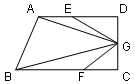 已知四边形ABCD是直角梯形,上底AD=8厘米,下底BC=10厘米,直角腰CD=6厘米,E是AD的中点,F是BC上的点,BF=
已知四边形ABCD是直角梯形,上底AD=8厘米,下底BC=10厘米,直角腰CD=6厘米,E是AD的中点,F是BC上的点,BF=| 2 | 3 |
26.7
26.7
平方厘米.分析:三角形ABG的面积=梯形的面积-三角形BCG的面积-三角形AGD的面积,而要求三角形BCG三角形AGD的面积,则要先求它们的高CG和DG,又因三角形DEG的面积与三角形CFG的面积相等,所以可以求出CG和DG,由此题目得解.
解答:解:设DG为h,则CG=6-h,
因:三角形DEG的面积与三角形CFG的面积相等;
即:4×h÷2=
×10×(6-h)÷2;
求得:h=
厘米,6-h=
厘米;
三角形AGD的面积=8×
÷2≈10.9平方厘米;
三角形BCG的面积=10×
÷2≈16.4平方厘米;
三角形ABG的面积=(10+8)×6÷2-10.9-16.4,
=26.7平方厘米;
故此题应填26.7.
因:三角形DEG的面积与三角形CFG的面积相等;
即:4×h÷2=
| 1 |
| 3 |
求得:h=
| 30 |
| 11 |
| 36 |
| 11 |
三角形AGD的面积=8×
| 30 |
| 11 |
三角形BCG的面积=10×
| 36 |
| 11 |
三角形ABG的面积=(10+8)×6÷2-10.9-16.4,
=26.7平方厘米;
故此题应填26.7.
点评:此题主要考查三角形和梯形的面积公式.

练习册系列答案
相关题目
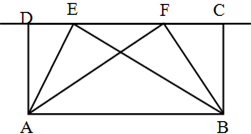 已知四边形ABCD是长方形,三角形ABE中的点E可以在线段CD上移动,如果E点移动到F上,三角形ABE和三角形ABF的面积分别为甲和乙,那么它们的大小关系是( )
已知四边形ABCD是长方形,三角形ABE中的点E可以在线段CD上移动,如果E点移动到F上,三角形ABE和三角形ABF的面积分别为甲和乙,那么它们的大小关系是( )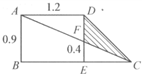
 已知四边形ABCD是正方形,边长为3,BE=1.5,AF=1,求阴影部分的面积(如图).
已知四边形ABCD是正方形,边长为3,BE=1.5,AF=1,求阴影部分的面积(如图).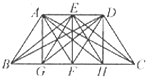 如图,已知四边形ABCD是一个等腰梯形,点E、F分别是上下两底的中点,点G、H分别是BF、CF的中点,且BC=2AD,则图中以A、B、C、D、E、F、G、H为顶点的所有三角形中,与△HEC面积相等的三角形有
如图,已知四边形ABCD是一个等腰梯形,点E、F分别是上下两底的中点,点G、H分别是BF、CF的中点,且BC=2AD,则图中以A、B、C、D、E、F、G、H为顶点的所有三角形中,与△HEC面积相等的三角形有