题目内容
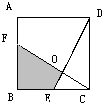已知四边形ABCD是正方形，边长为3，BE=1.5，AF=1，求阴影部分的面积（如图）．分析：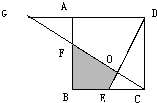
1．延长CF，设与DA交于一点G；
2．三角形AFG相似于三角形BFC，比例为BF：FA=2，可知AG=
BC=1.5；
3．三角形EOC相似于三角形DOG，比例为DG：EC=3，可知OGD的高是OEC高的三倍．若OEC的高为h，则h+3h=DC，DC=3，可知h=
．
4．阴影部分面积等于三角形BCF的面积减去三角形ECO的面积，带入数值，即可得解．
1．延长CF，设与DA交于一点G；2．三角形AFG相似于三角形BFC，比例为BF：FA=2，可知AG=
| 1 |
| 2 |
3．三角形EOC相似于三角形DOG，比例为DG：EC=3，可知OGD的高是OEC高的三倍．若OEC的高为h，则h+3h=DC，DC=3，可知h=
| 3 |
| 4 |
4．阴影部分面积等于三角形BCF的面积减去三角形ECO的面积，带入数值，即可得解．
解答：解：BF×BC÷2-EC×h÷2
=（3-1）×3÷2-（3-1.5）×
÷2
=2×3÷2-1.5×0.75÷2
=3-0.5625
=2.4375．
答：阴影部分的面积是2.4379．
=（3-1）×3÷2-（3-1.5）×
| 3 |
| 4 |
=2×3÷2-1.5×0.75÷2
=3-0.5625
=2.4375．
答：阴影部分的面积是2.4379．
点评：此题利用辅助线，两次三角形的相似，求出三角形ECO的高是解决此题的关键．
练习册系列答案
相关题目
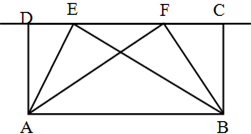已知四边形ABCD是长方形，三角形ABE中的点E可以在线段CD上移动，如果E点移动到F上，三角形ABE和三角形ABF的面积分别为甲和乙，那么它们的大小关系是（ ）
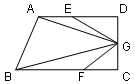已知四边形ABCD是直角梯形，上底AD=8厘米，下底BC=10厘米，直角腰CD=6厘米，E是AD的中点，F是BC上的点，BF=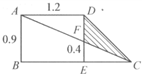
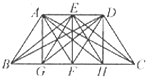如图，已知四边形ABCD是一个等腰梯形，点E、F分别是上下两底的中点，点G、H分别是BF、CF的中点，且BC=2AD，则图中以A、B、C、D、E、F、G、H为顶点的所有三角形中，与△HEC面积相等的三角形有