题目内容
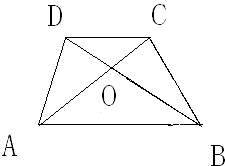 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=6,CD=4,梯形ABCD的面积为5,求三角形OBC的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=6,CD=4,梯形ABCD的面积为5,求三角形OBC的面积.分析:因为梯形的面积S=(a+b)×h÷2,所以梯形ABCD的高是5×2÷(6+4)=1,又因为AB∥CD,所以三角形OCD相似与三角形OAB,所以对应高的比等于对应的底的比,所以三角形ODC的高是
×1=
,由此求出三角形ODC的面积,进而求出三角形OBC的面积.
| 4 |
| 4+6 |
| 2 |
| 5 |
解答:解:梯形ABCD的高是:5×2÷(6+4)=1,
又因为AB∥CD,
所以三角形OCD相似与三角形OAB,
所以对应高的比等于对应的底的比,
三角形ODC的高是
×1=
,
三角形OBC的面积是4×1÷2-4×
÷2
=2-
=
;
答:三角形OBC的面积是
.
又因为AB∥CD,
所以三角形OCD相似与三角形OAB,
所以对应高的比等于对应的底的比,
三角形ODC的高是
| 4 |
| 4+6 |
| 2 |
| 5 |
三角形OBC的面积是4×1÷2-4×
| 2 |
| 5 |
=2-
| 4 |
| 5 |
=
| 6 |
| 5 |
答:三角形OBC的面积是
| 6 |
| 5 |
点评:本题主要是利用相似三角形的高的比等于对应底的比和梯形的面积公式及三角形的面积公式解决问题.

练习册系列答案
相关题目

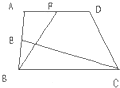 如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为
如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为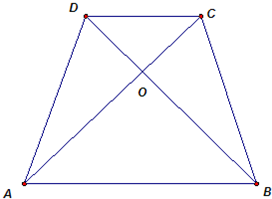 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.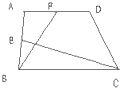 如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为________平方厘米.
如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为________平方厘米.