题目内容
 如右图,边长为10和12的两个正方形并放在一起,求三角形ABC(阴影部分)的面积.
如右图,边长为10和12的两个正方形并放在一起,求三角形ABC(阴影部分)的面积.分析:如图所示,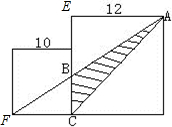 由图意及题目条件可以看出:FC:EA=CB:BE,即10:12=CB:BE,据此比例式即可求出CB的值,也就是阴影的底,这个底上的高已知,利用三角形的面积公式即可求解.
由图意及题目条件可以看出:FC:EA=CB:BE,即10:12=CB:BE,据此比例式即可求出CB的值,也就是阴影的底,这个底上的高已知,利用三角形的面积公式即可求解.
 由图意及题目条件可以看出:FC:EA=CB:BE,即10:12=CB:BE,据此比例式即可求出CB的值,也就是阴影的底,这个底上的高已知,利用三角形的面积公式即可求解.
由图意及题目条件可以看出:FC:EA=CB:BE,即10:12=CB:BE,据此比例式即可求出CB的值,也就是阴影的底,这个底上的高已知,利用三角形的面积公式即可求解.解答:解:设CB为x,则BE为12-x,
故有:10:12=x:(12-x),
12x=120-10x,
22x=120,
x=
;
阴影面积:
×12÷2=
=32
.
答:阴影部分的面积是32
.
故有:10:12=x:(12-x),
12x=120-10x,
22x=120,
x=
| 60 |
| 11 |
阴影面积:
| 60 |
| 11 |
| 360 |
| 11 |
| 8 |
| 11 |
答:阴影部分的面积是32
| 8 |
| 11 |
点评:此题主要考查组合图形的面积,关键是先求出阴影部分的底.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 如右图,边长为10和12的两个正方形并放在一起,求三角形ABC(阴影部分)的面积.
如右图,边长为10和12的两个正方形并放在一起,求三角形ABC(阴影部分)的面积.