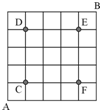
题目内容
 如图是5×5的网格.一只蚂蚁从网格左下角A点出发,沿网格线每次只能向上或者向右走一格,要到达右上角B点,且不能经过C、D、E和F点.则不同的走法共有
如图是5×5的网格.一只蚂蚁从网格左下角A点出发,沿网格线每次只能向上或者向右走一格,要到达右上角B点,且不能经过C、D、E和F点.则不同的走法共有30
30
种.分析:如下图所示,采用格点法,每点的走法都一一标出,左侧边和下边各个点都是只有一种走法,从下向上,第二行,c点不经过,它右边第一点有1种走法,第二点有2种走法,F点不走,它右边的点,只有1种走法;向上第三行,第二个点,只有左边来的1种走法,向右第三点,可以从左边和从下边走1+1=2,第四点,从左走2种加上从下边走的2种2+2=4种走法;因为F点不走,F上边的点只有从左边来的4种,再向右,右边第六点有左边的4种加上下边的1种,4+1=5种走法;向上的第四行,从左向右各点的走法依次1,1+1=2,2+2=4,4+4=8,8+4=12,12+5=17;继续向上的第五行,D点不经过,后面点依次有4,4+8=12,E点不经过,最右边的点只有从下边来的17种;最上一行,从左向右,依次有1,1,1+4=5,5+12=17,17;到达B的方法就是从左来的17种方法加上从下边来的17种方法,即可得解.
解答:解:如图所示,

17+17=34;
答:不同的走法共有34种;
故答案为:34.

17+17=34;
答:不同的走法共有34种;
故答案为:34.
点评:此题关键是在图形上逐点标出,从左边来的走法加上从下边来的走法就是该点的走法;如果有不经过的点,它右边的点,就只有从下边来的走法;它上边的点,就只有从左边来的走法;直到最后一点,是左边来的走法加上下边来的走法,即可得解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2009?和平区)如图是5×5的正方形网格图,设每个小方格的面积是1.A、B两点均在网格图中的交叉点上,A点的位置可用(2,3)表示,B点的位置可用(4,4)表示.现在要在网格图中的交叉点上找到C点,分别连接AB、BC、CA,使三角形ABC的面积为2.满足以上条件的C点在图上的不同位置分别用C1、C2、C3┅┅表示.如图所示,当C1的位置在(2,5)时,三解形ABC1的面积就是2.照样子,分别用C2、C3┅┅在右面网格图上以数对形式表示C点的其它所有可能位置.
(2009?和平区)如图是5×5的正方形网格图,设每个小方格的面积是1.A、B两点均在网格图中的交叉点上,A点的位置可用(2,3)表示,B点的位置可用(4,4)表示.现在要在网格图中的交叉点上找到C点,分别连接AB、BC、CA,使三角形ABC的面积为2.满足以上条件的C点在图上的不同位置分别用C1、C2、C3┅┅表示.如图所示,当C1的位置在(2,5)时,三解形ABC1的面积就是2.照样子,分别用C2、C3┅┅在右面网格图上以数对形式表示C点的其它所有可能位置. 如图是一个5×5的网格,每个小方格的面积都是1,阴影部分是类似数字“2”的图形,那么阴影部分的面积是
如图是一个5×5的网格,每个小方格的面积都是1,阴影部分是类似数字“2”的图形,那么阴影部分的面积是 如图是5×5的正方形网格图,设每个小方格的面积是1.A、B两点均在网格图中的交叉点上,A点的位置可用(2,3)表示,B点的位置可用(4,4)表示.现在要在网格图中的交叉点上找到C点,分别连接AB、BC、CA,使三角形ABC的面积为2.满足以上条件的C点在图上的不同位置分别用C1、C2、C3┅┅表示.如图所示,当C1的位置在(2,5)时,三解形ABC1的面积就是2.照样子,分别用C2、C3┅┅在右面网格图上以数对形式表示C点的其它所有可能位置.
如图是5×5的正方形网格图,设每个小方格的面积是1.A、B两点均在网格图中的交叉点上,A点的位置可用(2,3)表示,B点的位置可用(4,4)表示.现在要在网格图中的交叉点上找到C点,分别连接AB、BC、CA,使三角形ABC的面积为2.满足以上条件的C点在图上的不同位置分别用C1、C2、C3┅┅表示.如图所示,当C1的位置在(2,5)时,三解形ABC1的面积就是2.照样子,分别用C2、C3┅┅在右面网格图上以数对形式表示C点的其它所有可能位置.