题目内容
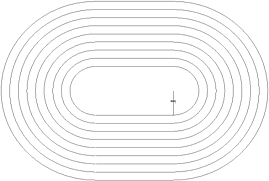 某中学计划建设一个400m跑道的运动场(如图所示),聘请你任工程师,问:
某中学计划建设一个400m跑道的运动场(如图所示),聘请你任工程师,问:
(1)若直道长100m,则弯道弧长半径r为多少m?
(2)共8个跑道,每条宽1.2m,操场最外圈长多少m?
(3)若操场中心铺绿草,跑道铺塑胶,则各需绿草、塑胶多少㎡?
(4)若绿草50元/㎡,塑胶350元/㎡,学校现有200万元,可以开工吗?为什么?
解:(1)(400-2×100)÷2÷3.14
=(400-200)÷2÷3.14
=200÷2÷3.14
=100÷3.14
≈31.85(m).
答:弯道弧长半径r为31.85m;
(2)2×3.14×(31.85+1.2×8)+100×2
=2×3.14×(31.85+9.6)+200
=3.14×82.9+200
=260.306+200
=460.306(m).
答:操场最外圈长460.306m;
(3)操场中心铺绿草的面积:
3.14×31.852+100×(31.85×2)
=3185.28665+6370
=9555.28665(㎡),
跑道铺塑胶的面积:
3.14×(31.85+1.2×8)2+100×[(31.85+1.2×8)×2]-9555.28665
=5394.84185+8290-9555.28665
=4129.5552(㎡).
答:需绿草9555.28665㎡、塑胶4129.5552㎡;
(4)9555.28665×50+4129.5552×350
=477764.3325+1445344.32
=1923108.6525(元).
因为200万元=2000000元>1923108.6525元,
答:学校现有200万元,可以开工.
分析:(1)先求出两个弯道弧长的长,再根据圆的周长变形公式:r=C÷π÷2,计算即可;
(2)根据圆的周长公式C=2πr,求出操场最外圈两个弯道弧长的长,加上两个直道长即为所求;
(3)操场中心铺绿草的面积=里面长方形的面积+里面两个半圆的面积;跑道铺塑胶的面积=外面长方形的面积+外面两个半圆的面积-操场中心铺绿草的面积,根据圆、圆环的面积公式和长方形的面积公式计算即可求解;
(4)分别求出操场中心铺绿草,跑道铺塑胶的钱数,相加后与200万元比较即可作出判断,注意单位的一致.
点评:考查了组合图形的面积,长方形的周长和面积,圆、圆环的周长和面积,本题关键是熟悉跑道的构造,同时本题计算量很大,要细心计算.
=(400-200)÷2÷3.14
=200÷2÷3.14
=100÷3.14
≈31.85(m).
答:弯道弧长半径r为31.85m;
(2)2×3.14×(31.85+1.2×8)+100×2
=2×3.14×(31.85+9.6)+200
=3.14×82.9+200
=260.306+200
=460.306(m).
答:操场最外圈长460.306m;
(3)操场中心铺绿草的面积:
3.14×31.852+100×(31.85×2)
=3185.28665+6370
=9555.28665(㎡),
跑道铺塑胶的面积:
3.14×(31.85+1.2×8)2+100×[(31.85+1.2×8)×2]-9555.28665
=5394.84185+8290-9555.28665
=4129.5552(㎡).
答:需绿草9555.28665㎡、塑胶4129.5552㎡;
(4)9555.28665×50+4129.5552×350
=477764.3325+1445344.32
=1923108.6525(元).
因为200万元=2000000元>1923108.6525元,
答:学校现有200万元,可以开工.
分析:(1)先求出两个弯道弧长的长,再根据圆的周长变形公式:r=C÷π÷2,计算即可;
(2)根据圆的周长公式C=2πr,求出操场最外圈两个弯道弧长的长,加上两个直道长即为所求;
(3)操场中心铺绿草的面积=里面长方形的面积+里面两个半圆的面积;跑道铺塑胶的面积=外面长方形的面积+外面两个半圆的面积-操场中心铺绿草的面积,根据圆、圆环的面积公式和长方形的面积公式计算即可求解;
(4)分别求出操场中心铺绿草,跑道铺塑胶的钱数,相加后与200万元比较即可作出判断,注意单位的一致.
点评:考查了组合图形的面积,长方形的周长和面积,圆、圆环的周长和面积,本题关键是熟悉跑道的构造,同时本题计算量很大,要细心计算.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
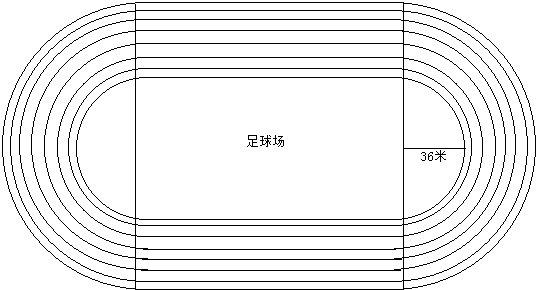
 某中学计划建设一个400m跑道的运动场(如图所示),聘请你任工程师,问:
某中学计划建设一个400m跑道的运动场(如图所示),聘请你任工程师,问: 一个半圆形花坛,周长为10.28米,面积为多少平方米?
一个半圆形花坛,周长为10.28米,面积为多少平方米?