题目内容
1. 一个半圆形花坛,周长为10.28米,面积为多少平方米?
一个半圆形花坛,周长为10.28米,面积为多少平方米?
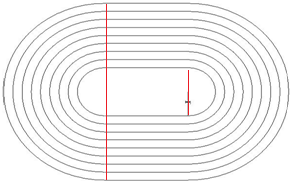
2.某中学计划建设一个400m跑道的运动场(如下图所示),聘请你任工程师,问:
(1)若直道长100m,则弯道弧长半径r为多少m?
(2)共8个跑道,每条宽1.2m,操场最外圈长多少m?
(3)若操场中心铺绿草,跑道铺塑胶,则各需绿草、塑胶多少㎡?
(4)若绿草50元/㎡,塑胶350元/㎡,学校现有200万元,可以开工吗?为什么?
 一个半圆形花坛,周长为10.28米,面积为多少平方米?
一个半圆形花坛,周长为10.28米,面积为多少平方米?2.某中学计划建设一个400m跑道的运动场(如下图所示),聘请你任工程师,问:
(1)若直道长100m,则弯道弧长半径r为多少m?
(2)共8个跑道,每条宽1.2m,操场最外圈长多少m?
(3)若操场中心铺绿草,跑道铺塑胶,则各需绿草、塑胶多少㎡?
(4)若绿草50元/㎡,塑胶350元/㎡,学校现有200万元,可以开工吗?为什么?
分析:1、要求这个半圆形花坛的面积,需要求得它的半径,设这个半圆形花坛的半径为x,根据周长公式即可列出方程解决问题;
2、(1)跑道两端的弯道合在一起正好组成一个圆形,它们的长度之和=这个跑道一圈的长度-两边直道的长度;利用圆的周长公式即可求得弯道的半径r;
(2)共8个跑道,每条宽1.2m,那么根据上面计算得出的内圈半径即可得出这个最外层弧长的半径,由此即可求得最外围的弧长,再加上两边直跑道的长度就是最外层跑道的周长;
(3)操场中心可以分成两部分两个半圆和一个长方形,利用圆的面积公式和长方形的面积公式,代入相关数据即可解决问题;用这个操场的面积-内部的面积就是跑道的面积,即需要塑胶多少平方米;
(4)利用上题中求得的草坪和塑胶的面积,即可计算得出总共需要的钱数,由此即可进行解答.
2、(1)跑道两端的弯道合在一起正好组成一个圆形,它们的长度之和=这个跑道一圈的长度-两边直道的长度;利用圆的周长公式即可求得弯道的半径r;
(2)共8个跑道,每条宽1.2m,那么根据上面计算得出的内圈半径即可得出这个最外层弧长的半径,由此即可求得最外围的弧长,再加上两边直跑道的长度就是最外层跑道的周长;
(3)操场中心可以分成两部分两个半圆和一个长方形,利用圆的面积公式和长方形的面积公式,代入相关数据即可解决问题;用这个操场的面积-内部的面积就是跑道的面积,即需要塑胶多少平方米;
(4)利用上题中求得的草坪和塑胶的面积,即可计算得出总共需要的钱数,由此即可进行解答.

解答:解:1、设这个半圆形花坛的半径为x,根据半圆的周长可得:
2x+3.14×x=10.28,
5.14x=10.28,
x=2,
3.14×22÷2=6.28(平方米),
答:这个半圆形花坛的面积是6.28平方米.
2、(1)600-2×100=200(米),
200÷3.14÷2≈32(米),
答:则弯道弧长半径为32米.
(2)3.14×(32+1.2×8)×2,
=3.14×41.6×2,
=261.248,
≈261(米),
261+100×2=461(米),
答:操场最外层的长度是461米.
(3)草坪的面积为:3.14×322+100×32,
=3.14×1024+3200,
=6415.36(平方米),
跑道的面积即需要塑胶的面积为:3.14×[(32+1.2×8)2-322]+100×1.2×8×2,
=3.14×706.56+1920,
=2218.5984+1920,
=4138.5984(平方米),
答:需要绿草的面积为6415.36平方米;需要塑胶4138.5984平方米.
(4)50×6415.36+320×4138.5984=1645119.488(元),
200万元>1645119.488元,
答:校现有200万元,可以开工.
2x+3.14×x=10.28,
5.14x=10.28,
x=2,
3.14×22÷2=6.28(平方米),
答:这个半圆形花坛的面积是6.28平方米.
2、(1)600-2×100=200(米),
200÷3.14÷2≈32(米),
答:则弯道弧长半径为32米.
(2)3.14×(32+1.2×8)×2,
=3.14×41.6×2,
=261.248,
≈261(米),
261+100×2=461(米),
答:操场最外层的长度是461米.
(3)草坪的面积为:3.14×322+100×32,
=3.14×1024+3200,
=6415.36(平方米),
跑道的面积即需要塑胶的面积为:3.14×[(32+1.2×8)2-322]+100×1.2×8×2,
=3.14×706.56+1920,
=2218.5984+1920,
=4138.5984(平方米),
答:需要绿草的面积为6415.36平方米;需要塑胶4138.5984平方米.
(4)50×6415.36+320×4138.5984=1645119.488(元),
200万元>1645119.488元,
答:校现有200万元,可以开工.
点评:此题考查了圆的面积与周长公式的灵活应用,这里要抓住环形跑道的特点,将这个环形跑道分成两端两个半圆,合在一起即是一个整圆,和中间一个长方形,这是解决本题的关键,本题的计算量较大,需要学生认真审题进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目