题目内容
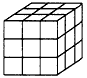
 一个立方体木块,6个面都涂上黑色,然后把它切成大小相等的27个小正方体,其中有三个面是黑色的小正方体有多少个?两面是黑色的有多少个?一面呢?没有涂上黑色的小正方体有多少块?
一个立方体木块,6个面都涂上黑色,然后把它切成大小相等的27个小正方体,其中有三个面是黑色的小正方体有多少个?两面是黑色的有多少个?一面呢?没有涂上黑色的小正方体有多少块?分析:根据题干可知:大正方体每条棱长上面都有3个小正方体;根据立体图形的知识可知:三个面均为红色的是各顶点处的小正方体,在各棱处,除去顶点处的正方体的有两面红色,在每个面上,除去棱上的正方体都是一面红色,所有的小正方体的个数减去有红色的小正方体的个数即是没有涂色的小正方体.根据上面的结论,即可求得答案.
解答:解:大正方体每条棱长上面都有3个小正方体;
所以三面涂色的都在顶点处,所以一共有8个.
两面涂色的有:(3-2)×12=1×12=12(个),
一面涂色的有:(3-2)×(3-2)×6,
=1×1×6,
=6(个),
没有涂色的有:27-6-12-8=1(个),
答:有三个面是黑色的小正方体有8个,两面是黑色的有12个,一面涂色的有6个,没有涂上黑色的小正方体有1个.
所以三面涂色的都在顶点处,所以一共有8个.
两面涂色的有:(3-2)×12=1×12=12(个),
一面涂色的有:(3-2)×(3-2)×6,
=1×1×6,
=6(个),
没有涂色的有:27-6-12-8=1(个),
答:有三个面是黑色的小正方体有8个,两面是黑色的有12个,一面涂色的有6个,没有涂上黑色的小正方体有1个.
点评:此题考查了立方体的知识.注意数形结合与正方体表面涂色的特点的应用.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目