题目内容
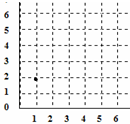 在方格图中有一个等腰直角三角形,顶角的顶点在(2,1)位置上,要使这个三角形的面积为2,则两个底角的顶点位置分别可以
在方格图中有一个等腰直角三角形,顶角的顶点在(2,1)位置上,要使这个三角形的面积为2,则两个底角的顶点位置分别可以(2,3)
(2,3)
:(4,1)
(4,1)
.分析:面积是2的等腰直角三角形,根据三角形的面积公式可知,这个三角形的底和高的乘积是2的2倍,既底×高=2×2=4,因这个三角形是等腰直角三角形,它的底和高分别是两条直角边且相等,据此可确定三角形的两条直角边分别是2和2.据此就可确定两个底角的顶点位置.
解答:解:根据三角形的面积公式可知,这个三角形的底和高的乘积是2的2倍,既底×高=2×2=4,
因这个三角形是等腰直角三角形,它的底和高分别是两条直角边且相等,
据此可确定三角形的两条直角边分别是2和2.
再由顶角的顶点的位置,即可确定两个底角的顶点位置分别(2,3),(4,1),
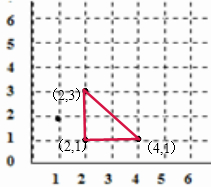
故答案为:(2,3),(4,1).
因这个三角形是等腰直角三角形,它的底和高分别是两条直角边且相等,
据此可确定三角形的两条直角边分别是2和2.
再由顶角的顶点的位置,即可确定两个底角的顶点位置分别(2,3),(4,1),

故答案为:(2,3),(4,1).
点评:本题的关键是确定直角三角形的两条直角边的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 在方格图中有一个等腰直角三角形,顶角的顶点在(2,1)位置上,要使这个三角形的面积为2,则两个底角的顶点位置分别可以________:________.
在方格图中有一个等腰直角三角形,顶角的顶点在(2,1)位置上,要使这个三角形的面积为2,则两个底角的顶点位置分别可以________:________.