题目内容
填空:
(1)一个棱长是4分米正方体容器装满水后,倒入一个底面积是12平方分米的圆锥体容器里正好装满,这个圆锥体的高是
(2)等底等高的一圆柱和一圆锥的体积之和是36立方分米,则圆锥的体积是
等底等高的一圆柱和一圆锥的体积之差是36立方分米,则圆柱的体积是
(1)一个棱长是4分米正方体容器装满水后,倒入一个底面积是12平方分米的圆锥体容器里正好装满,这个圆锥体的高是
16
16
分米.(2)等底等高的一圆柱和一圆锥的体积之和是36立方分米,则圆锥的体积是
9
9
立方分米.等底等高的一圆柱和一圆锥的体积之差是36立方分米,则圆柱的体积是
54
54
立方分米.分析:(1)根据题意,把正方体容器内的水倒入圆锥体容器里,水的体积的形状改变了,但是水的体积没有变,根据正方体的体积公式v=a3和圆锥的体积公式v=
sh,解答即可;
(2)等底等高的圆柱的体积是圆锥的体积的3倍,把它们的体积之和平均分成4份,则圆锥的体积就是其中1份,由此即可解决问题.
| 1 |
| 3 |
(2)等底等高的圆柱的体积是圆锥的体积的3倍,把它们的体积之和平均分成4份,则圆锥的体积就是其中1份,由此即可解决问题.
解答:解:(1)4×4×4=64(立方分米);
64÷
÷12
=64×3÷12,
=192÷12,
=16(分米);
答:这个圆锥体的高是16分米.
(2)36÷(3+1)=9(立方分米),
36÷(3-1)×3,
=36÷2×3,
=54(立方分米);
答:圆锥的体积是9立方分米;等底等高的一圆柱和一圆锥的体积之差是36立方分米,则圆柱的体积是54立方分米;
故答案为:16,9,54.
64÷
| 1 |
| 3 |
=64×3÷12,
=192÷12,
=16(分米);
答:这个圆锥体的高是16分米.
(2)36÷(3+1)=9(立方分米),
36÷(3-1)×3,
=36÷2×3,
=54(立方分米);
答:圆锥的体积是9立方分米;等底等高的一圆柱和一圆锥的体积之差是36立方分米,则圆柱的体积是54立方分米;
故答案为:16,9,54.
点评:此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 根据图中数据填空.
根据图中数据填空. 都是棱长为1厘米的正方体.
都是棱长为1厘米的正方体.
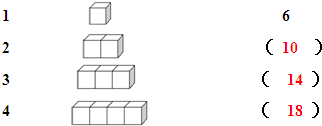
 找规律填空.
找规律填空.


