题目内容
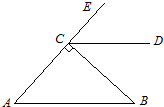如图，BC⊥AE，垂足为点C，过点C作CD∥AB．若∠ECD=48°，求∠B的度数．
解：因为BC⊥AE，
所以∠ECB=90°，
所以∠BCD=90°-∠ECD=90°-48°=42°，
因为CD∥AB，
所以∠B=∠BCD=42°，
答：∠B的度数是42°．
分析：因为BC⊥AE，所以∠ECB=90°；∠BCD=90°-∠ECD=90°-48°=42°又因为CD∥AB，所以∠B=∠BCD=42°．
点评：本题用到的知识点是：互相垂直的两条直线所成的夹角是90°；两条直线平行，内错角相等．
所以∠ECB=90°，
所以∠BCD=90°-∠ECD=90°-48°=42°，
因为CD∥AB，
所以∠B=∠BCD=42°，
答：∠B的度数是42°．
分析：因为BC⊥AE，所以∠ECB=90°；∠BCD=90°-∠ECD=90°-48°=42°又因为CD∥AB，所以∠B=∠BCD=42°．
点评：本题用到的知识点是：互相垂直的两条直线所成的夹角是90°；两条直线平行，内错角相等．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
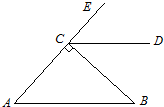如图，BC⊥AE，垂足为点C，过点C作CD∥AB．若∠ECD=48°，求∠B的度数．
