题目内容
用同样大小的两张长方形纸围成的圆柱,体积一定相等.
×
×
.(判断对错)分析:用长方形围成圆柱体,有两种不同的围法,一种是以长为高,一种是以宽为高,据此举出实例计算出它们的面积即可解答问题.
解答:解:假设这两个长方形的长都是4、宽都是2,
若第一个长方形以长为高,围成的圆柱的体积是:
π×(2÷π÷2)2×4,
=π×
×4,
=
,
第二个长方形以宽为高,围成的圆柱体的体积是:
π×(4÷π÷2)2×2,
=π×
×2,
=
,
所以围成的这两个圆柱体的体积不相等,原题说法错误.
故答案为:×.
若第一个长方形以长为高,围成的圆柱的体积是:
π×(2÷π÷2)2×4,
=π×
| 1 |
| π2 |
=
| 4 |
| π |
第二个长方形以宽为高,围成的圆柱体的体积是:
π×(4÷π÷2)2×2,
=π×
| 4 |
| π2 |
=
| 8 |
| π |
所以围成的这两个圆柱体的体积不相等,原题说法错误.
故答案为:×.
点评:此题主要考查圆柱体的侧面展开图的特征以及圆柱体的体积公式的计算应用.

练习册系列答案
相关题目
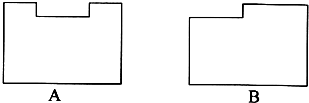
 (2009?自贡)用同样大小的黑、白两种小方砖铺一张正方形桌面,桌面的两条对角线铺黑色的小方砖,其余的都铺白色小方砖,如图所示.铺满这张桌面恰好用了93块黑色小方砖,那么用白色小方砖的块数是2116块.
(2009?自贡)用同样大小的黑、白两种小方砖铺一张正方形桌面,桌面的两条对角线铺黑色的小方砖,其余的都铺白色小方砖,如图所示.铺满这张桌面恰好用了93块黑色小方砖,那么用白色小方砖的块数是2116块.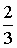 折了一只仙鹤,小明用同样大的一张纸的
折了一只仙鹤,小明用同样大的一张纸的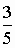 折了一只青蛙.
折了一只青蛙.
 。
。
 ,那么,从右面看到的是
,那么,从右面看到的是