题目内容
 (2009?自贡)用同样大小的黑、白两种小方砖铺一张正方形桌面,桌面的两条对角线铺黑色的小方砖,其余的都铺白色小方砖,如图所示.铺满这张桌面恰好用了93块黑色小方砖,那么用白色小方砖的块数是2116块.
(2009?自贡)用同样大小的黑、白两种小方砖铺一张正方形桌面,桌面的两条对角线铺黑色的小方砖,其余的都铺白色小方砖,如图所示.铺满这张桌面恰好用了93块黑色小方砖,那么用白色小方砖的块数是2116块.正确
正确
.分析:此题可以看做是方阵问题进行解决:那么根据实心方阵的特点可知每边点数为:(93+1)÷2=47,利用实心方阵总点数=每边点数×每边点数,先求得黑白方砖的总块数数为:47×47=2209块,由此计算得出白色小方砖即可进行判断.为:2009-93=2116(块)
解答:解:根每条边上的方砖块数为:(93+1)÷2=47(块)
黑白色点数之和为:47×47=2209(块),
所以白色方砖的块数为:2209-93=2116(块),
所以原题说法正确.
故答案为:正确.
黑白色点数之和为:47×47=2209(块),
所以白色方砖的块数为:2209-93=2116(块),
所以原题说法正确.
故答案为:正确.
点评:此题考查了利用实心方阵问题解决实际问题的灵活应用,这里抓住对角线上的块数之和得出每边点数是解决此类问题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 (2009?自贡)数对(2,4)表示玉兰坐在教室里的第4行第2列,那么浴缸坐在第5列,第6行可以用数对
(2009?自贡)数对(2,4)表示玉兰坐在教室里的第4行第2列,那么浴缸坐在第5列,第6行可以用数对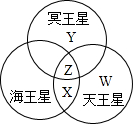 (2009?自贡)用圆圈表示星球上的空气,个星球上的空气所含的不同气体用不同的字母表示,相同的气体用相同的字母表示(如图).已知天王星与海王星上的空气中都含有氦气,冥王星上没有.那么图中字母( )表示氦气.
(2009?自贡)用圆圈表示星球上的空气,个星球上的空气所含的不同气体用不同的字母表示,相同的气体用相同的字母表示(如图).已知天王星与海王星上的空气中都含有氦气,冥王星上没有.那么图中字母( )表示氦气.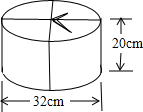 (2009?自贡)奶奶过生日,妈妈去蛋糕店买了一盒蛋糕给奶奶祝贺生日,为了方便携带,蛋糕店的工人用漂亮的彩色丝带包扎(如图,图中的粗线为彩色丝带),接头处一共用去30厘米,包扎这盒蛋糕一共用了多少厘米的彩色丝带?
(2009?自贡)奶奶过生日,妈妈去蛋糕店买了一盒蛋糕给奶奶祝贺生日,为了方便携带,蛋糕店的工人用漂亮的彩色丝带包扎(如图,图中的粗线为彩色丝带),接头处一共用去30厘米,包扎这盒蛋糕一共用了多少厘米的彩色丝带?