题目内容
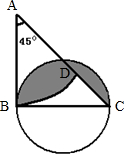
已知三角形ABC面积是12平方厘米,求阴影部分的面积?

解:设等腰直角三角形ABC的直角边为a,
 a2=12,a2=24;
a2=12,a2=24;
扇形ABD的面积: πa2=3π=9.42(平方厘米),
πa2=3π=9.42(平方厘米),
空白部分BCD的面积:12-9.42=2.58(平方厘米),
半圆面积: π(a÷2)2=
π(a÷2)2= ×3.14×24=9.42(平方厘米),
×3.14×24=9.42(平方厘米),
阴影面积:9.42-2.58=6.84(平方厘米);
答:阴影部分面积是6.84平方厘米.
分析:要求阴影部分的面积,可用半圆面积减去里面的空白面积,求空白面积可用三角形面积减去扇形面积.
点评:此题主要考查求阴影部分的面积,可以按一般思路去解答,就是用半圆面积减去里面的空白面积,而空白面积可用三角形面积减去扇形面积.
 a2=12,a2=24;
a2=12,a2=24;扇形ABD的面积:
 πa2=3π=9.42(平方厘米),
πa2=3π=9.42(平方厘米),空白部分BCD的面积:12-9.42=2.58(平方厘米),
半圆面积:
 π(a÷2)2=
π(a÷2)2= ×3.14×24=9.42(平方厘米),
×3.14×24=9.42(平方厘米),阴影面积:9.42-2.58=6.84(平方厘米);
答:阴影部分面积是6.84平方厘米.
分析:要求阴影部分的面积,可用半圆面积减去里面的空白面积,求空白面积可用三角形面积减去扇形面积.
点评:此题主要考查求阴影部分的面积,可以按一般思路去解答,就是用半圆面积减去里面的空白面积,而空白面积可用三角形面积减去扇形面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如下图,已知三角形ABC面积是1平方厘米,延长AB至D,使BD=AB,延长BC至E,使CE=2BC,延长CA至F,使AF=3AC,求三角形DEF的面积.
如下图,已知三角形ABC面积是1平方厘米,延长AB至D,使BD=AB,延长BC至E,使CE=2BC,延长CA至F,使AF=3AC,求三角形DEF的面积.