题目内容
 如下图,已知三角形ABC面积是1平方厘米,延长AB至D,使BD=AB,延长BC至E,使CE=2BC,延长CA至F,使AF=3AC,求三角形DEF的面积.
如下图,已知三角形ABC面积是1平方厘米,延长AB至D,使BD=AB,延长BC至E,使CE=2BC,延长CA至F,使AF=3AC,求三角形DEF的面积.分析:连接AE和CD,要求三角形DEF的面积,可以分成三部分来分别计算,如下图所示:
此题关键是利用高一定时,三角形的面积与高对应的底成正比的关系进行计算的;三角形ABC是一个重要的条件,抓住图形中与它同高的三角形进行分析计算,即可解得下面大三角形的面积.

此题关键是利用高一定时,三角形的面积与高对应的底成正比的关系进行计算的;三角形ABC是一个重要的条件,抓住图形中与它同高的三角形进行分析计算,即可解得下面大三角形的面积.

解答:解:因为BD=AB,
所以S△ABC=S△BCD=1(平方厘米);则S△ACD=1+1=2(平方厘米),
因为AF=3AC,所以FC=4AC,
所以S△FCD=4S△ACD=4×2=8(平方厘米),
同理可以求得:
S△ACE=2S△ABC=2(平方厘米),则S△FCE=4S△ACE=4×2=8(平方厘米);
S△DCE=2S△BCD=2×1=2(平方厘米);
所以S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18(平方厘米),
答:三角形DEF的面积是18平方厘米.
所以S△ABC=S△BCD=1(平方厘米);则S△ACD=1+1=2(平方厘米),
因为AF=3AC,所以FC=4AC,
所以S△FCD=4S△ACD=4×2=8(平方厘米),
同理可以求得:
S△ACE=2S△ABC=2(平方厘米),则S△FCE=4S△ACE=4×2=8(平方厘米);
S△DCE=2S△BCD=2×1=2(平方厘米);
所以S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18(平方厘米),
答:三角形DEF的面积是18平方厘米.
点评:此题考查了高相等时,三角形的面积与底成正比的关系在实际问题中的灵活应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
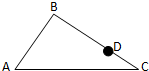 (2012?广州)如下图,有一条三角形的环路,A至B是上坡路,B至C是下坡路,A至C是平路,AB、BC、AC三段距离的比是3:4:5.乐乐和扬扬同时从A出发,乐乐按顺时针方向行走,扬扬按逆时针方向行走,2.5小时后在D点相遇.已知两人上坡速度都是4千米/小时,下坡速度都是6千米/小时,在平路上速度都是5千米/小时.
(2012?广州)如下图,有一条三角形的环路,A至B是上坡路,B至C是下坡路,A至C是平路,AB、BC、AC三段距离的比是3:4:5.乐乐和扬扬同时从A出发,乐乐按顺时针方向行走,扬扬按逆时针方向行走,2.5小时后在D点相遇.已知两人上坡速度都是4千米/小时,下坡速度都是6千米/小时,在平路上速度都是5千米/小时. 如下图,有一条三角形的环路,A至B是上坡路,B至C是下坡路,A至C是平路,AB、BC、AC三段距离的比是3:4:5.乐乐和扬扬同时从A出发,乐乐按顺时针方向行走,扬扬按逆时针方向行走,2.5小时后在D点相遇.已知两人上坡速度都是4千米/小时,下坡速度都是6千米/小时,在平路上速度都是5千米/小时.
如下图,有一条三角形的环路,A至B是上坡路,B至C是下坡路,A至C是平路,AB、BC、AC三段距离的比是3:4:5.乐乐和扬扬同时从A出发,乐乐按顺时针方向行走,扬扬按逆时针方向行走,2.5小时后在D点相遇.已知两人上坡速度都是4千米/小时,下坡速度都是6千米/小时,在平路上速度都是5千米/小时.