题目内容
 如图所示,已知APBCD是以直线|为对称轴的图形,且∠APD=116°,∠DPC=40°,DC>AB,那么,以A、P、B、C和D五个点为顶点的所有三角形中有
如图所示,已知APBCD是以直线|为对称轴的图形,且∠APD=116°,∠DPC=40°,DC>AB,那么,以A、P、B、C和D五个点为顶点的所有三角形中有6
6
个钝角三角形,有4
4
个锐角三角形.分析:根据三角形的分类:有一个角是钝角的三角形,叫钝角三角形;三个角都是锐角的三角形,叫锐角三角形;进行解答即可.
解答:解:
=10,以A、P、B、C、D五个点可以形成10个三角形,这10个三角形的内角中,
∠APD=∠BPC=116°>90°,∠APC=∠BPD=116°+40=156>90°
∵DC>AB,故∠ADC与∠BCD为锐角,∠BAD与∠ABC为钝角,
∠APB=360°-116°×2-40°=88°<90°,
其余均为锐角,故有6个钝角三角形,4个锐角三角形;
故答案为:6,4.
| C | 3 5 |
∠APD=∠BPC=116°>90°,∠APC=∠BPD=116°+40=156>90°
∵DC>AB,故∠ADC与∠BCD为锐角,∠BAD与∠ABC为钝角,
∠APB=360°-116°×2-40°=88°<90°,
其余均为锐角,故有6个钝角三角形,4个锐角三角形;
故答案为:6,4.
点评:此题考查了三角形的分类的方法以及运用.

练习册系列答案
相关题目
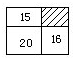 一块长方形耕地如图所示,已知其中三块小长方形的面积分别是15、16、20亩,则阴影部分的面积是
一块长方形耕地如图所示,已知其中三块小长方形的面积分别是15、16、20亩,则阴影部分的面积是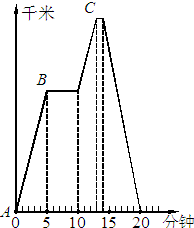 一辆汽车从A站出发经过B站到C站,然后按原路返回,汽车行驶的路程与时间关系如图所示.已知汽车从A站到C站每小时行60千米.那么汽车从C站返回A站的速度是每小时行
一辆汽车从A站出发经过B站到C站,然后按原路返回,汽车行驶的路程与时间关系如图所示.已知汽车从A站到C站每小时行60千米.那么汽车从C站返回A站的速度是每小时行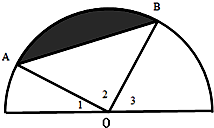 如图所示,已知∠1:∠2:∠3=1:3:2,△ABO的面积是12平方厘米,求阴影部分的面积.
如图所示,已知∠1:∠2:∠3=1:3:2,△ABO的面积是12平方厘米,求阴影部分的面积. 在广州亚运会上,某一天统计我国已获得金牌、银牌、铜牌数量的情况如图所示.已知这时的铜牌总数是96枚,那么金牌是多少枚?
在广州亚运会上,某一天统计我国已获得金牌、银牌、铜牌数量的情况如图所示.已知这时的铜牌总数是96枚,那么金牌是多少枚?