题目内容
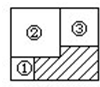 如图,大长方形的面积是小于200的整数,它的内部有三个边长是整数的正方形,正方形③的边长是长方形长的
如图,大长方形的面积是小于200的整数,它的内部有三个边长是整数的正方形,正方形③的边长是长方形长的| 7 |
| 16 |
| 1 |
| 4 |
53
53
.分析:据题意可知:正方形②的边长是长方形长的1-
=
,而正方形②的边长又是长方形宽的1-
=
;
:
=4:3,则长方形的长、宽比为4:3; 长方形的面积=
宽×宽<200,宽×宽<150; 宽=12,长=16,据此可以分别求出三个正方形的面积,长方形的面积减三个正方形的面积,就是阴影部分的面积.
| 7 |
| 16 |
| 9 |
| 16 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 16 |
| 4 |
| 3 |
解答:解:因为正方形②的边长是长方形长的1-
=
,而正方形②的边长又是长方形宽的1-
=
;
:
=4:3,则长方形的长、宽比为4:3; 长方形的面积=×
宽×宽<200,宽×宽<150; 宽=12,长=16,
则长方形的面积=12×16=192;
正方形1的面积=
×
=9;
正方形3面积=(16×
)×(16×
)=49;
正方形2的面积=(12×
)×(12×
)=81;
所以阴影部分的面积=192-9-49-81=53.
故答案为:53.
| 7 |
| 16 |
| 9 |
| 16 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 16 |
| 4 |
| 3 |
则长方形的面积=12×16=192;
正方形1的面积=
| 12 |
| 4 |
| 12 |
| 4 |
正方形3面积=(16×
| 7 |
| 16 |
| 7 |
| 16 |
正方形2的面积=(12×
| 3 |
| 4 |
| 3 |
| 4 |
所以阴影部分的面积=192-9-49-81=53.
故答案为:53.
点评:此题主要考查组合图形的面积.关键是先求出长方形的长和宽.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
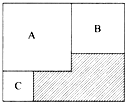 如图,大长方形的面积是小于200的整数,内部有三个边长为整数的正方形A,B,
如图,大长方形的面积是小于200的整数,内部有三个边长为整数的正方形A,B, (2013?青羊区模拟)如图,大长方形的面积是600平方厘米,它的周长是
(2013?青羊区模拟)如图,大长方形的面积是600平方厘米,它的周长是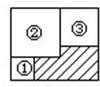 如图,大长方形的面积是小于200的整数,它的内部有三个边长是整数的正方形,正方形③的边长是长方形长的
如图,大长方形的面积是小于200的整数,它的内部有三个边长是整数的正方形,正方形③的边长是长方形长的 ,正方形①的边长是长方形宽的
,正方形①的边长是长方形宽的 ,那么图中阴影部分的面积是________.
,那么图中阴影部分的面积是________.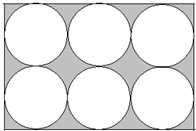 如图,大长方形的面积是600平方厘米,它的周长是________厘米.
如图,大长方形的面积是600平方厘米,它的周长是________厘米.