Question

操作题：
（1）在方格图中标出A（2，1）、B（8，1）、C（8，7）、D（2，7）的点并顺次连成封闭图形ABCD
（2）在四边形ABCD内分别以AB、BC边为直径画半圆，并画出这个组合图形的对称轴．
（3）将图中两个半圆重叠部分涂上阴影，若每个小方格的边长是2厘米，则图中阴影部分的面积是

20.52

平方厘米．（写出必要的过程）．

Answer 1

分析：（1）在图中分别找出A、B、C、D四个点，再顺次连接即可得到图形ABCD；
（2）以AB、BC边为直径画半圆，连接BD即为这个组合图形的对称轴；
（3）用直径是6×2厘米的半圆的面积减去底是6×2厘米高是3×2厘米的三角形ABE的面积求出阴影部分的面积．

解答：解：（1）（2）如图：

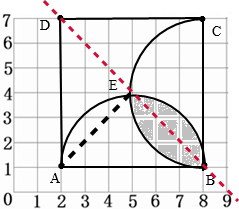
（3）3.14×（6×2÷2）²÷2-6×2×3×2÷2，
=3.14×18-36，
=56.52-36，
=20.52（平方厘米），
答：图中阴影部分的面积是20.52平方厘米．
故答案为：20.52．

点评：本题主要考查了数对的意义及组合图形的对称轴的作法和组合图形的面积的计算方法．