题目内容
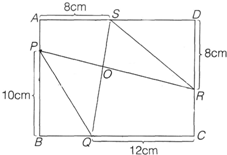如图，在长方形ABCD的四条边AB、BC、CD、DA上分别取P、Q、R、S四点，设PR和QS的交点为O．当三角形PQO的面积和三角形RSO的面积都等于30cm2时，请求出长方形ABCD的面积．考点：长方形、正方形的面积,三角形的周长和面积
专题：平面图形的认识与计算
分析：观察图形可知：设AP=x，BQ=y，分别用梯形的面积公式表示出同学ABQS和梯形APRD的面积，进而推论得出这两个梯形的面积之差就等于三角形PBQ和三角形SRD的面积之差，进而利用等量代换的方法求出长方形的长和宽的值，再据长方形的面积公式即可求解．
解答：
解：设AP=x，BQ=y，
则 梯形ABQS面积=（8+y）（10+x）÷2=（80+10y+8x+xy）÷2①；
梯形APRD面积=（8+x）（12+y）÷2=（96+8y+12x+xy）÷2②；
因为梯形ABQS面积-梯形APRD面积
=面积PBQO-面积SORD
=面积PBQ-面积SRD （因为面积POQ=面积SOR）
=（10y÷2）-8（12+y-8）÷2
=5y-16-4y
=y-16；
又因①-②=[-16+2y-4x]÷2
=y-2x-8
所以y-16=y-2x-8
得：x=4
所以RC=10+4-8=6
进而求出BQ=5
所以长方形ABCD的面积为：
（5+12）×（8+6）
=17×14
=238（平方厘米）．
答：长方形ABCD的面积是238平方厘米．
则 梯形ABQS面积=（8+y）（10+x）÷2=（80+10y+8x+xy）÷2①；
梯形APRD面积=（8+x）（12+y）÷2=（96+8y+12x+xy）÷2②；
因为梯形ABQS面积-梯形APRD面积
=面积PBQO-面积SORD
=面积PBQ-面积SRD （因为面积POQ=面积SOR）
=（10y÷2）-8（12+y-8）÷2
=5y-16-4y
=y-16；
又因①-②=[-16+2y-4x]÷2
=y-2x-8
所以y-16=y-2x-8
得：x=4
所以RC=10+4-8=6
进而求出BQ=5
所以长方形ABCD的面积为：
（5+12）×（8+6）
=17×14
=238（平方厘米）．
答：长方形ABCD的面积是238平方厘米．
点评：此题是一道超难的奥数题，需要依据面积的转换，多方面思考，求出长方形的长和宽的值，再据长方形的面积公式求解．
练习册系列答案
相关题目