题目内容
如图，直角等腰三角形ABC的斜边BC长8厘米，将这个三角形以顶点A为定点，沿顺时针方向旋转90度，那么斜边BC扫过的面积是多少平方厘米？
解：根据题干分析，设这个圆的半径是r，
三角形BCD的面积是：8×8÷2=32（平方厘米），
所以2r×r÷2=32，
则r2=32，
所以半圆的面积是：3.14×32÷2=50.24（平方厘米），
则阴影部分的面积是：50.24-32=18.24（平方厘米）；
答：BC边划过的面积是18.24平方厘米．
分析：根据题干可以画出这个旋转后的示意图；将这个三角形以顶点A为定点，沿顺时针方向旋转90度，则斜边BC扫过的面积就是图中涂色部分的面积，即等于半圆的面积-直角三角形BCD的面积，由此即可分析解答．
点评：根据题干，画出这个等腰直角三角形旋转后的图形，再利用半圆和三角形的面积公式即可解答问题．
三角形BCD的面积是：8×8÷2=32（平方厘米），
所以2r×r÷2=32，
则r2=32，
所以半圆的面积是：3.14×32÷2=50.24（平方厘米），
则阴影部分的面积是：50.24-32=18.24（平方厘米）；
答：BC边划过的面积是18.24平方厘米．
分析：根据题干可以画出这个旋转后的示意图；将这个三角形以顶点A为定点，沿顺时针方向旋转90度，则斜边BC扫过的面积就是图中涂色部分的面积，即等于半圆的面积-直角三角形BCD的面积，由此即可分析解答．
点评：根据题干，画出这个等腰直角三角形旋转后的图形，再利用半圆和三角形的面积公式即可解答问题．
练习册系列答案
名校课堂系列答案
相关题目
如图，直角等腰三角形ABC的斜边BC长8厘米，将这个三角形以顶点A为定点，沿顺时针方向旋转90度，那么斜边BC扫过的面积是多少平方厘米？
（2011?河池）如图是一个等腰三角形，面积是5平方分米．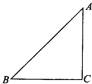
如图，ABC是一个直角等腰三角形，直角边的长度是1米．现在以C点为圆心，把三角形ABC顺时针旋转90度，那么，AB边在旋转时所扫过的面积是
如图是一个等腰三角形，面积是5平方分米．