题目内容
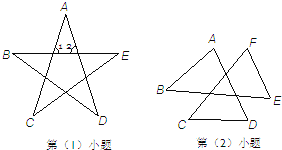
【题目】(1)如图1,∠A+∠B+∠C+∠D+∠E= ,∠1+∠2= °
(2)如图2,∠A+∠B+∠C+∠D+∠E+∠F= .
【答案】180°,144°,360°.
【解析】
试题分析:(1)根据三角形的内角和定理和三角形的外角和定理进行解答,因为∠1=∠C+∠E,∠2=∠B+∠D,所以∠1+∠2+∠A=180°,所以∠A+∠B+∠C+∠D+∠E=180°.
因为∠A=∠B=∠C=∠D=∠E,所以∠A=36°,所以∠1+∠2=180°﹣∠A=180°﹣36°=144°
(2)根据三角形的内角和定理进行解答,用三个大三角形的内角和减去中间小三角形的内角和,即180°×3﹣180°=360°
解:(1)因为∠1=∠C+∠E,∠2=∠B+∠D
所以∠1+∠2+∠A=180°
所以∠A+∠B+∠C+∠D+∠E=180°
又因为∠A=∠B=∠C=∠D=∠E
所以∠A=180°÷5=36°
所以∠1+∠2=180°﹣∠A=180°﹣36°=144°
(2)180°×3﹣180°=360°

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目