题目内容
有一个算式(如图1),式中画的“□”代表被擦掉的数字,其中m,n分别为积的万位、千位上的数字,设m×n的个位数字是p,如图2,梯形ABCD是直角梯形,上底AD=m厘米,下底BC=n厘米,直角腰CD=P厘米,E是AD中点,F是BC上的点,且CF:BF=1:2,G是CD上的点,若三角形BFG的面积与三角AEG的面积相等,试求图2中阴影部分的面积.
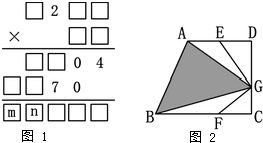

分析:(1)因第一个因数的个位与第二个因数的十位的乘积的末位是0,第一个因数个位与第二个因数个位的乘积是4,可确定的第二个因数的十位是5,又5与第一个因数的个位和十位的乘积是70,可确定第一个因数的后两位是14或34,是14时与第一个因数个位的乘积是04,不合题意,当是34时,第二个因数的个位是6符合题意,又因第二个因数的十位与第一个因数的乘积是四位数,可确定第一个因数的千位是1,所以第一个因数是1234,第二个因数是56,可求出m和n是多少;
(2)由(1)可求出p是多少,可求出p是多少,然后,再根据高相等的三角形的面积的比就是它们高的比,可滶出CG的高,然后再用梯形的面积减去空白部分的面积,就是阴影部分的面积.据此解答.
(2)由(1)可求出p是多少,可求出p是多少,然后,再根据高相等的三角形的面积的比就是它们高的比,可滶出CG的高,然后再用梯形的面积减去空白部分的面积,就是阴影部分的面积.据此解答.
解答:解:(1)根据分析知:第一个因数是1234,第二个因数是56,字谜填写如下:
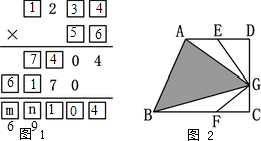
(2)m=6,n=9,6×9=54,
所以P=4.CD=4厘米,
CF:BF=1:2,BC=CF+BF=9(厘米),
所以CF=3厘米,BF=6厘米,
E是AD中点,AD=6厘米,
所以AE=ED=3厘米,
三角形BFG的面积与三角AEG的面积相等,
所以S△EDG=2S△CFG,
S△EDG:S△CFG=2:1,
DG:CG=2:1,
(CD-CG):CG=2:1,
(4-CG):CG=2:1,
CG=
(厘米),
S△BCG=9×
÷2=6(平方厘米),
S△ADG=6×(4-
)÷2=8(平方厘米),
阴影部分的面积是:
(6+9)×4÷2-8-6,
=15×4÷2-8-6,
=30-8-6,
=16(平方厘米);
答:阴影部分的面积是16平方厘米.

(2)m=6,n=9,6×9=54,
所以P=4.CD=4厘米,
CF:BF=1:2,BC=CF+BF=9(厘米),
所以CF=3厘米,BF=6厘米,
E是AD中点,AD=6厘米,
所以AE=ED=3厘米,
三角形BFG的面积与三角AEG的面积相等,
所以S△EDG=2S△CFG,
S△EDG:S△CFG=2:1,
DG:CG=2:1,
(CD-CG):CG=2:1,
(4-CG):CG=2:1,
CG=
| 4 |
| 3 |
S△BCG=9×
| 4 |
| 3 |
S△ADG=6×(4-
| 4 |
| 3 |
阴影部分的面积是:
(6+9)×4÷2-8-6,
=15×4÷2-8-6,
=30-8-6,
=16(平方厘米);
答:阴影部分的面积是16平方厘米.
点评:本题的关键是根据乘法的计算方法进行推理求出两个因数分别是多少,再确定m和n的值,然后确定P是多少,再求出CG是多少,然后根据阴影部分的面积=梯形的面积-空白部分的面积,求出阴部部分的面积.

练习册系列答案
相关题目
 (2008?高邮市)列算式(或方程),并计算.
(2008?高邮市)列算式(或方程),并计算. 找规律填空.
找规律填空.



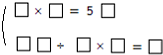 如图的两道算式由1~9这九个数字组成,其中有一个数字已经知道,请你将其余的数字填入空格,使算式成立.
如图的两道算式由1~9这九个数字组成,其中有一个数字已经知道,请你将其余的数字填入空格,使算式成立. 找规律填空.
找规律填空.


