题目内容
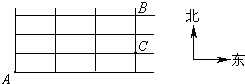如图是一个道路图，A处有一大群孩子，这群孩子向东或向北走，在从A开始的每个路口，都有一半人向北走，另一半人向东走，如果先后有60个孩子到过路口B，则先后共有48
48
个孩子到过路口C．分析：把A处孩子的孩子数量是看成单位“1”，运用表示法，找出B处的孩子数几分之几，C处的孩子数是几分之几，然后根据B处的孩子数60人对应的分率，求出孩子的总数，进而求出C处的孩子数．
解答：解：把A处孩子的孩子数量是看成单位“1”，那么标数可得：
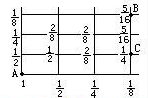
B处孩子占孩子总数的
，所以孩子总数是：
60÷
=192（人）
C处的孩子数是：192×
=48（人）
答：先后共有48个孩子到过路口C．
故答案为：48．
B处孩子占孩子总数的
| 5 |
| 16 |
60÷
| 5 |
| 16 |
C处的孩子数是：192×
| 1 |
| 4 |
答：先后共有48个孩子到过路口C．
故答案为：48．
点评：本题也可以这样求解：假设A处有1个孩子，2个孩子时有什么问题，发现后来就会出现半个孩子的情况，这是不行的，所以再假设有4个，8个，16个孩子，发现后来还是会出现半个孩子，于是我们就假设A处有32个孩子吧，最后经过计算能发现C处有8个孩子经过，B处有10个孩子经过．但事实上B处有60个孩子经过，所以原来A处就应该是6个32个孩子，所以就有8×6=48个孩子经过C点．
练习册系列答案
相关题目
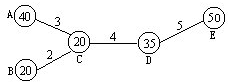如图是A，B，C，D，E五个村之间的道路示意图，○中数字是各村要上学的学生人数，道路上的数表示两村之间的距离（单位：千米）．现在要在五村之中选一个村建立一所小学．为使所有学生到学校的总距离最短，试确定最合理的方案．
