题目内容
【题目】按要求画一画,填一填。(每个小方格的面积是![]() )
)
(1)已知点A的位置用数对表示是(2,6),则点B的位置用数对表示是( )。
(2)画出三角形![]() 绕点B顺时针旋转90°后的图形。
绕点B顺时针旋转90°后的图形。
(3)画出三角形![]() 按3∶1的比放大后的图形。
按3∶1的比放大后的图形。
(4)如果点B点C不动,点A向左平移2格,三角形![]() 将变成一个( )三角形,它与原三角形相比,面积( )。
将变成一个( )三角形,它与原三角形相比,面积( )。
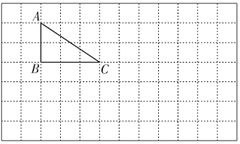
【答案】(1)(2,4)
(2)(3)如图
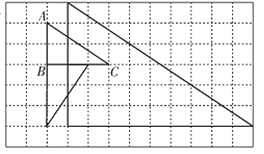
(4)钝;不变
【解析】
(1)根据数对的表示方法,第一个数字表示列,第二个数字表示行,据此可得解;
(2)根据旋转的特征,点B不动,其余各点均绕点B按顺时针方向旋转90°;
(3)按照3∶1的比例将三角形放大后,三角形的低和高分别扩大到原来的3倍,据此画图即可;
(4)原来的三角形是直角三角形,当A向右平移2个格后,![]() 变大,三角形变成了钝角三角形,但变化后的三角形与原三角形的底和高相等,所以面积也相等。
变大,三角形变成了钝角三角形,但变化后的三角形与原三角形的底和高相等,所以面积也相等。
(1)已知点A的位置用数对表示是(2,6),表示第二列第六行,B在A的下面两个格,表示第二列第四行,所以B用数对表示是(2,4);
(2)找出原三角形的三个关键点,再画出![]() 绕点B顺时针旋转90°后的图形即可;
绕点B顺时针旋转90°后的图形即可;
(3)据分析可知,在图中画出底为9cm宽为8厘米的三角形;
(4)据分析可知,变成了钝角三角形,变化后的三角形与原三角形的底和高相等,所以面积也相等。
故答案为:(1)(2,4)
(2)(3)如图
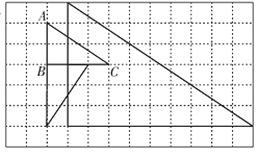
(4)钝;不变

练习册系列答案
相关题目