题目内容
对于任意自然数a、b定义运算是a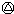 b=(a+b)÷2;若a、b奇偶性不同,则a
b=(a+b)÷2;若a、b奇偶性不同,则a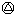 b=(a+b+1)÷2.求(1997
b=(a+b+1)÷2.求(1997 1998)
1998)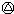 (1998
(1998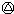 1999)(1999
1999)(1999 2000)
2000)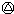 (2000
(2000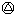 2001)
2001)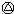 (2001
(2001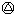 2002)=_
2002)=_
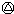 b=(a+b)÷2;若a、b奇偶性不同,则a
b=(a+b)÷2;若a、b奇偶性不同,则a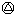 b=(a+b+1)÷2.求(1997
b=(a+b+1)÷2.求(1997 1998)
1998)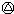 (1998
(1998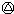 1999)(1999
1999)(1999 2000)
2000)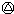 (2000
(2000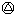 2001)
2001)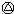 (2001
(2001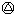 2002)=_
2002)=_2002
2002
.分析:根据题意,可知如果两个数的奇偶性相同,定义的新运算是这两个数的和除以2;如果两个数的奇偶性不同,定义的新运算就是这两个数的和再加上1所得的结果除以2;然后再根据题意进一步计算即可.
解答:解:根据题意可得:
1997与1998的奇偶性不同;
1997 1998=(1997+1998+1)÷2=1998;
1998=(1997+1998+1)÷2=1998;
同理:1998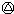 1999=1999,1999
1999=1999,1999 2000=2000,2000
2000=2000,2000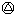 2001=2001,2001
2001=2001,2001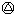 2002=2002;
2002=2002;
所以,
(1997 1998)
1998)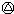 (1998
(1998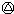 1999)
1999)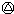 (1999
(1999 2000)
2000)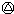 (2000
(2000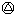 2001)
2001)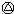 (2001
(2001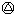 2002)
2002)
=1998 1999
1999 2000
2000 2001
2001 2002
2002
=1999 2000
2000 2001
2001 2002
2002
=2000 2001
2001 2002
2002
=2001 2002
2002
=2002.
故答案为:2002.
1997与1998的奇偶性不同;
1997
 1998=(1997+1998+1)÷2=1998;
1998=(1997+1998+1)÷2=1998;同理:1998
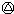 1999=1999,1999
1999=1999,1999 2000=2000,2000
2000=2000,2000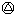 2001=2001,2001
2001=2001,2001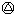 2002=2002;
2002=2002;所以,
(1997
 1998)
1998)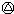 (1998
(1998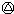 1999)
1999)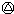 (1999
(1999 2000)
2000)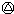 (2000
(2000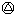 2001)
2001)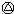 (2001
(2001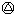 2002)
2002)=1998
 1999
1999 2000
2000 2001
2001 2002
2002=1999
 2000
2000 2001
2001 2002
2002=2000
 2001
2001 2002
2002=2001
 2002
2002=2002.
故答案为:2002.
点评:本题的关键是先判断两个数的奇偶,然后再根据定义的新运算进行计算即可.

练习册系列答案
相关题目