题目内容
将如图（1）所示的三角形纸片沿粗虚线折叠成如图（2）所示的图形．已知图（1）三角形的面积是图（2）图形面表的1.5倍，图（2）中阴影部分的面积之和为1平方厘米．求重叠部分的面积．分析：已知图（1）三角形的面积是图（2）图形面表的1.5倍，又由图（2）可知，重叠部分面积加阴影部分等于图（1）的面积，因此，重叠部分是图（1）的0.5倍，则阴影部分面积也是图形（1）的0.5倍，又知中阴影部分的面积之和为1平方厘米，因此，图（1）的面积是2平方厘米，重叠部分面积是2平方厘米-1平方厘米=1平方厘米．
解答：解：重叠部分面积是图（1）面积的：1.5-1=0.5倍，
因此，阴影部分面也是图（1）面积的0.5倍，
又知影部分的面积之和为1平方厘米，
所以图（1）面积的1÷0.5=2（平方厘米），
所以重叠部分的面积是2平方厘米-1平方厘米=1平方厘米．
答：重叠部分的面积是1平方厘米．
因此，阴影部分面也是图（1）面积的0.5倍，
又知影部分的面积之和为1平方厘米，
所以图（1）面积的1÷0.5=2（平方厘米），
所以重叠部分的面积是2平方厘米-1平方厘米=1平方厘米．
答：重叠部分的面积是1平方厘米．
点评：本题是考查简单图形的折叠问题，关键是明白重叠部分面积加阴影部分等于图（1）的面积，重叠部分是图（1）的0.5倍，阴影部分面积也是图形（1）的0.5倍，从而求得阴影部分面积．
练习册系列答案
相关题目
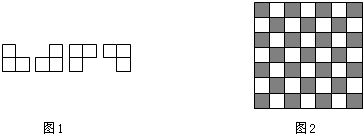
有三个圆心相同的半圆，它们的直径分别为1、3、5，用线段将其分割成9块，如图所示，如果每块中的字母代表着这一块面积，并且相同字母表示相同的面积，那么A：B=