题目内容
【题目】从一块长12cm、宽9cm、高6cm的长方体陶泥上切下一个最大的正方体，剩下部分的表面积与原长方体的表面积相比，会怎样变化？列出你想到的所有情况。
【答案】①以长方体的一个顶点为正方体的一个顶点切：表面积减小72平方厘米；
②不挨顶点，沿棱切：表面积不变。
③从长方体里边切，不挨顶点和棱：表面积增加72平方厘米
【解析】
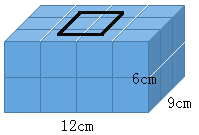，如图，从一块长12cm、宽9cm、高6cm的长方体陶泥上切下一个最大的正方体，正方体的棱长是6厘米，①以长方体的一个顶点为正方体的一个顶点切，表面积减少了两个正方体的面；②不挨顶点，沿棱切：表面积不变；③从长方体里边切，不挨顶点和棱，表面积增加两个正方体的面，据此分析。
①以长方体的一个顶点为正方体的一个顶点切：表面积减小，6×6×2＝72（平方厘米）。
②不挨顶点，沿棱切：表面积不变。
③从长方体里边切，不挨顶点和棱：表面积增加，6×6×2＝72（平方厘米）
练习册系列答案
阅读快车系列答案
相关题目
